University of Phoenix - DAT/305 - Individual: Recursion, Section 5.3Resource: Ch. 5, "Recursion", of Data Structures: Abstraction and Design Using Java, Exercises for Section 5.3; Self-Check #4Complet
Chapter 5
Recursion
Chapter Objectives
To understand how to think recursively
To learn how to trace a recursive method
To learn how to write recursive algorithms and methods for searching arrays
To learn about recursive data structures and recursive methods for a LinkedList class
To understand how to use recursion to solve the Towers of Hanoi problem
To understand how to use recursion to process two-dimensional images
To learn how to apply backtracking to solve search problems such as finding a path through a maze
This chapter introduces a programming technique called recursion and shows you how to think recursively. You can use recursion to solve many kinds of programming problems that would be very difficult to conceptualize and solve without recursion. Computer scientists in the field of artificial intelligence (AI) often use recursion to write programs that exhibit intelligent behavior: playing games such as chess, proving mathematical theorems, recognizing patterns, and so on.
In the beginning of the chapter, you will be introduced to recursive thinking and how to design a recursive algorithm and prove that it is correct. You will also learn how to trace a recursive method and use activation frames for this purpose.
Recursive algorithms and methods can be used to perform common mathematical operations, such as computing a factorial or a greatest common divisor(gcd). Recursion can be used to process familiar data structures, such as strings, arrays, and linked lists, and to design a very efficient array search technique called binary search. You will also see that a linked list is a recursive data structure and learn how to write recursive methods that perform common list-processing tasks.
Recursion can be used to solve a variety of other problems. The case studies in this chapter use recursion to solve a game, to search for “blobs” in a two-dimensional image, and to find a path through a maze.
Recursion
5.1 Recursive Thinking
5.2 Recursive Definitions of Mathematical Formulas
5.3 Recursive Array Search
5.4 Recursive Data Structures
5.5 Problem Solving with Recursion
Case Study: Towers of Hanoi
Case Study: Counting Cells in a Blob
5.6 Backtracking
Case Study: Finding a Path through a Maze
5.1 Recursive Thinking
Recursion is a problem-solving approach that can be used to generate simple solutions to certain kinds of problems that would be difficult to solve in other ways. In a recursive algorithm, the original problem is split into one or more simpler versions of itself. For example, if the solution to the original problem involved n items, recursive thinking might split it into two problems: one involving n − 1 items and one involving just a single item. Then the problem with n − 1 items could be split again into one involving n − 2 items and one involving just a single item, and so on. If the solution to all the one-item problems is “trivial,” we can build up the solution to the original problem from the solutions to the simpler problems.
As an example of how this might work, consider a collection of nested wooden figures as shown in Figure 5.1. If you wanted to write an algorithm to “process” this collection in some way (such as counting the figures or painting a face on each figure), you would have difficulty doing it because you don't know how many objects are in the nest. But you could use recursion to solve the problem in the following way.
Recursive Algorithm to Process Nested Figures
1. if there is one figure in the nest
2. Do whatever is required to the figure.
else
3. Do whatever is required to the outer figure in the nest.
4. Process the nest of figures inside the outer figure in the same way.
image
FIGURE 5.1 A Set of Nested Wooden Figures
In this recursive algorithm, the solution is trivial if there is only one figure: perform Step 2. If there is more than one figure, perform Step 3 to process the outer figure. Step 4 is the recursive operation—recursively process the nest of figures inside the outer figure. This nest will, of course, have one less figure than before, so it is a simpler version of the original problem.
As another example, let's consider searching for a target value in an array. Assume that the array elements are sorted and are in increasing order. A recursive approach, which we will study in detail in Section 5.3, involves replacing the problem of searching an array of n elements with one of searching an array of n/2 elements. How do we do that? We compare the target value to the value of the element in the middle of the sorted array. If there is a match, we have found the target. If not, based on the result of the comparison, we either search the elements that come before the middle one or the elements that come after the middle one. So we have replaced the problem of searching an array with n elements to one that involves searching a smaller array with only n/2 elements. The recursive algorithm follows.
Recursive Algorithm to Search an Array
1. if the array is empty
2. Return –1 as the search result.
else if the middle element matches the target
3. Return the subscript of the middle element as the result.
else if the target is less than the middle element
4. Recursively search the array elements before the middle element and return the result.
else
5. Recursively search the array elements after the middle element and return the result.
The condition in Step 1 is true when there are no elements left to search. Step 2 returns –1 to indicate that the search failed. Step 3 executes when the middle element matches the target. Otherwise, we recursively apply the search algorithm (Steps 4 and 5), thereby searching a smaller array (approximately half the size), and return the result. For each recursive search, the region of the array being searched will be different, so the middle element will also be different.
The two recursive algorithms we showed so far follow this general approach:
General Recursive Algorithm
1. if the problem can be solved for the current value of n
2. Solve it.
else
3. Recursively apply the algorithm to one or more problems involving smaller values of n.
4. Combine the solutions to the smaller problems to get the solution to the original.
Step 1 involves a test for what is called the base case: the value of n for which the problem can be solved easily. Step 3 is the recursive case because we recursively apply the algorithm. Because the value of n for each recursive case is smaller than the original value of n, each recursive case makes progress toward the base case. Whenever a split occurs, we revisit Step 1 for each new problem to see whether it is a base case or a recursive case.
Steps to Design a Recursive Algorithm
From what we have seen so far, we can summarize the characteristics of a recursive solution:
There must be at least one case (the base case), for a small value of n, that can be solved directly.
A problem of a given size (say, n) can be split into one or more smaller versions of the same problem (the recursive case).
Therefore, to design a recursive algorithm, we must
Recognize the base case and provide a solution to it.
Devise a strategy to split the problem into smaller versions of itself. Each recursive case must make progress toward the base case.
Combine the solutions to the smaller problems in such a way that each larger problem is solved correctly.
Next, we look at a recursive algorithm for a common programming problem. We will also provide a Java method that solves this problem. All of the methods in this section and in the next will be found in class RecursiveMethods.java on this textbook's Web site.
EXAMPLE 5.1
Let's see how we could write our own recursive method for finding the string length. How would you go about doing this? If there is a special character that marks the end of a string, then you can count all the characters that precede this special character. But if there is no special character, you might try a recursive approach. The base case is an empty string—its length is 0. For the recursive case, consider that each string has two parts: the first character and the “rest of the string.” If you can find the length of the “rest of the string,” you can then add 1 (for the first character) to get the length of the larger string. For example, the length of "abcde" is 1 + the length of "bcde".
Recursive Algorithm for Finding the Length of a String
1. if the string is empty (has no characters)
2. The length is 0.
else
3. The length is 1 plus the length of the string that excludes the first character.
We can implement this algorithm as a static method with a String argument. The test for the base case is a string reference of null or a string that contains no characters (""). In either case, the length is 0. In the recursive case,
return 1 + length(str.substring(1));
the method call str.substring(1) returns a reference to a string containing all characters in string str except for the character at position 0. Then we call method length again with this substring as its argument. The method result is one more than the value returned from the next call to length. Each time we reenter the method length, the if statement executes with str referencing a string containing all but the first character in the previous call. Method length is called a recursive method because it calls itself.
/** Recursive method length (in RecursiveMethods.java).
@param str The string
@return The length of the string
*/
public static int length(String str) {
if (str == null || str.isEmpty())
return 0;
else
return 1 + length(str.substring(1));
EXAMPLE 5.2
Method printChars is a recursive method that displays each character in its string argument on a separate line. In the base case (an empty or nonexistent string), the method return occurs immediately and nothing is displayed. In the recursive case, printChars displays the first character of its string argument and then calls itself to display the characters in the rest of the string. If the initial call is printChars("hat"), the method will display the lines
h
a
t
Unlike the method length in Example 5.1, printChars is a void method. However, both methods follow the format for the general recursive algorithm shown earlier.
/** Recursive method printChars (in RecursiveMethods.java).
post: The argument string is displayed, one character per line.
@param str The string
*/
public static void printChars(String str) {
if (str == null || str.isEmpty()) {
return;
} else {
System.out.println(str.charAt(0));
printChars(str.substring(1));
}
}
You get an interesting result if you reverse the two statements in the recursive case.
/** Recursive method printCharsReverse (in RecursiveMethods.java).
post: The argument string is displayed in reverse,
one character per line.
@param str The string
*/
public static void printCharsReverse(String str) {
if (str == null || str.isEmpty()) {
return;
} else {
printCharsReverse(str.substring(1));
System.out.println(str.charAt(0));
}
}
Method printCharsReverse calls itself to display the rest of the string before displaying the first character in the current string argument. The effect will be to delay displaying the first character in the current string until all characters in the rest of the string are displayed. Consequently, the characters in the string will be displayed in reverse order. If the initial call is printCharsReverse("hat"), the method will display the lines
t
a
Proving that a Recursive Method Is Correct
To prove that a recursive method is correct, you must verify that you have performed correctly the design steps listed earlier. You can use a technique that mathematicians use to prove that a theorem is true for all values of n. A proof by induction works the following way:
Prove the theorem is true for the base case of (usually) n = 0 or n = 1.
Show that if the theorem is assumed true for n, then it must be true for n + 1.
We can extend the notion of an inductive proof and use it as the basis for proving that a recursive algorithm is correct. To do this:
Verify that the base case is recognized and solved correctly.
Verify that each recursive case makes progress toward the base case.
Verify that if all smaller problems are solved correctly, then the original problem is also solved correctly.
If you can show that your algorithm satisfies these three requirements, then your algorithm will be correct.
EXAMPLE 5.3
To prove that the length method is correct, we know that the base case is an empty string and its length is correctly set at 0. The recursive case involves a call to length with a smaller string, so it is making progress toward the base case. Finally, if we know the length of the rest of the string, adding 1 gives us the length of the longer string consisting of the first character and the rest of the string.
Tracing a Recursive Method
Figure 5.2 traces the execution of the method call length("ace"). The diagram shows a sequence of recursive calls to the method length. After returning from each call to length, we complete execution of the statement return 1 + length(…); by adding 1 to the result so far and then returning from the current call. The final result, 3, would be returned from the original call. The arrow alongside each word return shows which call to length is associated with that result. For example, 0 is the result of the method call length(""). After adding 1, we return 1, which is the result of the call length("e"), and so on. This process of returning from the recursive calls and computing the partial results is called unwinding the recursion.
image
FIGURE 5.2 Trace of length("ace")
The Run-Time Stack and Activation Frames
You can also trace a recursive method by showing what Java does when one method calls another. Java maintains a run-time stack, on which it saves new information in the form of an activation frame. The activation frame contains storage for the method arguments and any local variables as well as the return address of the instruction that called the method. Whenever a method is called, Java pushes a new activation frame onto the run-time stack and saves this information on the stack. This is done whether or not the method is recursive.
The left side of Figure 5.3 shows the activation frames on the run-time stack after the last recursive call (corresponding to length("")) resulting from an initial call to length("ace"). At any given time, only the frame at the top of the stack is accessible, so its argument values will be used when the method instructions execute. When the return statement executes, control will be passed to the instruction at the specified return address, and this frame will be popped from the stack (Figure 5.3, right). The activation frame corresponding to the next-to-last call (length("e")) is now accessible.
image
FIGURE 5.3 Run-Time Stack before and after Removal of Frame for length("")
You can think of the run-time stack for a sequence of calls to a recursive method as an office tower in which an employee on each floor has the same list of instructions1. The employee in the bottom office carries out part of the instructions on the list, calls the employee in the office above, and is put on hold. The employee in the office above starts to carry out the list of instructions, calls the employee in the next higher office, is put on hold, and so on. When the employee on the top floor is called, that employee carries out the list of instructions to completion and then returns an answer to the employee below. The employee below then resumes carrying out the list of instructions and returns an answer to the employee on the next lower floor, and so on, until an answer is returned to the employee in the bottom office, who then resumes carrying out the list of instructions.
To make the flow of control easier to visualize, we will draw the activation frames from the top of the page down (see Figure 5.4). For example, the activation frame at the top, which would actually be at the bottom of the run-time stack, represents the first call to the recursive method. The downward-pointing arrows connect each statement that calls a method with the frame for that particular execution of the method. The upward-pointing arrows show the return point from each lower-level call with the value returned alongside the arrow. For each frame, the return point is to the addition operator in the statement return 1 + length(…);. For each frame, the code in the gray screen is executed prior to the creation of the next activation frame; the rest of the code shown is executed after the return.
image
FIGURE 5.4 Trace of length("ace") Using Activation Frames
EXERCISES FOR SECTION 5.1
SELF-CHECK
Trace the execution of the call mystery(4) for the following recursive method using the technique shown in Figure 5.2. What does this method do?
public static mystery(int n) {
if (n == 0)
return 0;
else
return n * n + mystery(n – 1);
}
Answer Exercise 1 above using activation frames.
Trace the execution of printChars("tic") (Example 5.2) using activation frames.
Trace the execution of printCharsReverse("toc") using activation frames.
Prove that the printChars method is correct.
Trace the execution of length("tictac") using a diagram like Figure 5.2.
Write a recursive algorithm that determines whether a specified target character is present in a string. It should return true if the target is present and false if it is not. The stopping steps should be
a string reference to null or a string of length 0, the result is false
the first character in the string is the target, the result is true.
The recursive step would involve searching the rest of the string.
PROGRAMMING
Write a recursive method toNumber that forms the integer sum of all digit characters in a string. For example, the result of toNumber("3ac4") would be 7. Hint: If next is a digit character ('0' through '9'), Character.isDigit(next) is true and the numeric value of next is Character.digit(next, 10).
Write a recursive method stutter that returns a string with each character in its argument repeated. For example, if the string passed to stutter is "hello", stutter will return the string "hheelllloo".
Write a recursive method that implements the recursive algorithm for searching a string in Self-Check Exercise . The method heading should be public static boolean searchString(String str, char ch)
5.2 Recursive Definitions of Mathematical Formulas
Mathematicians often use recursive definitions of formulas. These definitions lead very naturally to recursive algorithms.
EXAMPLE 5.4
The factorial of n, or n!, is defined as follows:
0!=1n!=n×(n−1)!
The first formula identifies the base case: n equal to 0. The second formula is a recursive definition. It leads to the following algorithm for computing n!.
Recursive Algorithm for Computing n!
1. if n equals 0
2. n! is 1.
else
3. n! = n × (n – 1)!
To verify the correctness of this algorithm, we see that the base case is solved correctly (0! is 1). The recursive case makes progress toward the base case because it involves the calculation of a smaller factorial. Also, if we can calculate (n – 1)!, the recursive case gives us the correct formula for calculating n!.
The recursive method follows. The statement
return n * factorial(n – 1);
implements the recursive case. Each time factorial calls itself, the method body executes again with a different argument value. An initial method call such as factorial(4) will generate four recursive calls, as shown in Figure 5.5.
/** Recursive factorial method (in RecursiveMethods.java).
pre: n >= 0
@param n The integer whose factorial is being computed
@return n!
*/
public static int factorial(int n) {
if (n == 0)
return 1;
else
return n * factorial(n – 1);
image
FIGURE 5.5 Trace of factorial(4)
image PITFALL
Infinite Recursion and Stack Overflow
If you call method factorial with a negative argument, you will see that the recursion does not terminate. It will continue forever because the stopping case, n equals 0, can never be reached, as n gets more negative with each call. For example, if the original value of n is –4, you will make method calls factorial(–5), factorial(–6), factorial(–7), and so on. You should make sure that your recursive methods are constructed so that a stopping case is always reached. One way to prevent the infinite recursion in this case would be to change the terminating condition to n <= 0. However, this would incorrectly return a value of 1 for n! if n is negative. A better solution would be to throw an IllegalArgumentException if n is negative.
If your program does not terminate properly, you may see an extremely long display on the console (if the console is being used to display its results). Eventually the exception StackOverflowError will be thrown. This means that the memory area used to store information about method calls (the run-time stack) has been used up because there have been too many calls to the recursive method. Because there is no memory available for this purpose, your program can't execute any more method calls.
EXAMPLE 5.5
Let's develop a recursive method that raises a number x to a power n, where n is positive or zero. You can raise a number to a power by repeatedly multiplying that number by itself. So if we know xk, we can get xk+1 by multiplying xk by x. The recursive definition is
xn=x×xn–1
This gives us the recursive case. You should know that any number raised to the power 0 is 1, so the base case is
x0=1
Recursive Algorithm for Calculating xn (n ≥ 0)
1. if n is 0
2. The result is 1.
else
3. The result is x×xn–1
.
We show the method next.
/** Recursive power method (in RecursiveMethods.java).
pre: n >= 0
@param x The number being raised to a power
@param n The exponent
@return x raised to the power n
*/
public static double power(double x, int n) {
if (n == 0)
return 1;
else
return x * power(x, n – 1);
EXAMPLE 5.6
The greatest common divisor (gcd) of two numbers is the largest integer that divides both numbers. For example, the gcd of 20, 15 is 5; the gcd of 36, 24 is 12; the gcd of 36, 18 is 18. The mathematician Euclid devised an algorithm for finding the greatest common divisor (gcd) of two integers, m and n, based on the following definition.
Definition of gcd(m, n) for m > n
gcd(m, n) = n if n is a divisor of m
gcd(m, n) = gcd(n, m % n) if n isn't a divisor of m
This definition states that gcd(m, n) is n if n divides m. This is correct because no number larger than n can divide n. Otherwise, the definition states that gcd(m, n) is the same as gcd(n, m % n), where m % n is the integer remainder of m divided by n. Therefore, gcd(20, 15) is the same as gcd(15, 5), or 5, because 5 divides 15. This recursive definition leads naturally to a recursive algorithm.
Recursive Algorithm for Calculating gcd(m, n) for m > n
1. if n is a divisor of m
2. The result is n.
else
3. The result is gcd(n, m % n).
To verify that this is correct, we need to make sure that there is a base case and that it is solved correctly. The base case is “n is a divisor of m.” If so, the solution is n (n is the gcd), which is correct. Does the recursive case make progress to the base case? It must because both arguments in each recursive call are smaller than in the previous call, and the new second argument is always smaller than the new first argument (m % n must be less than n). Eventually a divisor will be found, or the second argument will become 1. Since 1 is a base case (1 divides every integer), we have verified that the recursive case makes progress toward the base case.
Next, we show method gcd. Note that we do not need a separate clause to handle arguments that initially are not in the correct sequence. This is because if m < n, then m % n is m and the recursive call will transpose the arguments so that m > n in the first recursive call.
/** Recursive gcd method (in RecursiveMethods.java).
pre: m > 0 and n > 0
@param m The larger number
@param n The smaller number
@return Greatest common divisor of m and n
*/
public static double gcd(int m, int n) {
if (m % n == 0)
return n;
else
return gcd(n, m % n);
Tail Recursion versus Iteration
Method gcd above is an example of tail recursion. In tail recursion, the last thing a method does is to call itself. You may have noticed that there are some similarities between tail recursion and iteration. Both techniques enable us to repeat a compound statement. In iteration, a loop repetition condition in the loop header determines whether we repeat the loop body or exit from the loop. We repeat the loop body while the repetition condition is true. In tail recursion, the condition usually tests for a base case. In a recursive method, we stop the recursion when the base case is reached (the condition is true), and we execute the method body again when the condition is false.
We can always write an iterative solution to any problem that is solvable by recursion. However, the recursive solutions will be easier to conceptualize and should, therefore, lead to methods that are easier to write, read, and debug—all of which are very desirable attributes of code.
EXAMPLE 5.7
In Example 5.4, we wrote the recursive method.
public static int factorial(int n) {
if (n == 0)
return 1;
else
return n * factorial(n – 1);
}
It is a straightforward process to turn this method into an iterative one, replacing the if statement with a loop, as we show next.
/** Iterative factorial method.
pre: n >= 0
@param n The integer whose factorial is being computed
@return n!
*/
public static int factorialIter(int n) {
int result = 1;
while (n > 0){
result *= n;
n = n - 1;
}
return result;
Efficiency of Recursion
The iterative method factorialIter multiplies all integers between 1 and n to compute n!. It may be slightly less readable than the recursive method factorial, but not much. In terms of efficiency, both algorithms are O(n) because the number of loop repetitions or recursive calls increases linearly with n. However, the iterative version is probably faster because the overhead for a method call and return would be greater than the overhead for loop repetition (testing and incrementing the loop control variable). The difference, though, would not be significant. Generally, if it is easier to conceptualize an algorithm using recursion, then you should code it as a recursive method because the reduction in efficiency does not outweigh the advantage of readable code that is easy to debug.
EXAMPLE 5.8
The Fibonacci numbers fibn are a sequence of numbers that were invented to model the growth of a rabbit colony. Therefore, we would expect this sequence to grow very quickly, and it does. For example, fib10 is 55, fib15 is 610, fib20 is 6765, and fib25 is 75,025 (that's a lot of rabbits!). The definition of this sequence follows:
fib0=0fib1=1fibn=fibn−1+fibn−2
Next, we show a method that calculates the nth Fibonacci number. The last line codes the recursive case.
/** Recursive method to calculate Fibonacci numbers
(in RecursiveMethods.java).
pre: n >= 0
@param n The position of the Fibonacci number being calculated
@return The Fibonacci number
*/
public static int fibonacci(int n) {
if (n == 0)
return 0;
else if (n == 1)
return 1;
else
return fibonacci(n – 1) + fibonacci(n – 2);
}
Unfortunately, this solution is very inefficient because of multiple calls to fibonacci with the same argument. For example, calculating fibonacci(5) results in calls to fibonacci(4) and fibonacci(3). Calculating fibonacci(4) results in calls to fibonacci(3) (second call) and also fibonacci(2). Calculating fibonacci(3) twice results in two more calls to fibonacci(2) (three calls total), and so on (see Figure 5.6).
image
FIGURE 5.6 Method Calls Resulting from fibonacci(5)
Because of the redundant method calls, the time required to calculate fibonacci(n) increases exponentially with n. For example, if n is 100, there are approximately 2100 activation frames. This number is approximately 1030. If you could process one million activation frames per second, it would still take 1024 seconds, which is approximately 3 × 1016 years. However, it is possible to write recursive methods for computing Fibonacci numbers that have O(n) performance. We show one such method next.
/** Recursive O(n) method to calculate Fibonacci numbers
(in RecursiveMethods.java).
pre: n >= 1
@param fibCurrent The current Fibonacci number
@param fibPrevious The previous Fibonacci number
@param n The count of Fibonacci numbers left to calculate
@return The value of the Fibonacci number calculated so far
*/
private static int fibo(int fibCurrent, int fibPrevious, int n) {
if (n == 1)
return fibCurrent;
else
return fibo(fibCurrent + fibPrevious, fibCurrent, n – 1);
}
Unlike method fibonacci, method fibo does not follow naturally from the recursive definition of the Fibonacci sequence. In the method fibo, the first argument is always the current Fibonacci number and the second argument is the previous one. We update these values for each new call. When n is 1 (the base case), we have calculated the required Fibonacci number, so we return its value (fibCurrent). The recursive case
return fibo(fibCurrent + fibPrevious, fibCurrent, n – 1);
passes the sum of the current Fibonacci number and the previous Fibonacci number to the first parameter (the new value of fibCurrent); it passes the current Fibonacci number to the second parameter (the new value of fibPrevious); and it decrements n, making progress toward the base case.
To start this method executing, we need the following wrapper method, which is not recursive. This method is called a wrapper method because its main purpose is to call the recursive method and return its result. Its parameter, n, specifies the position in the Fibonacci sequence of the number we want to calculate. After testing for the special case n equals 0, it calls the recursive method fibo, passing the first Fibonacci number as its first argument and n as its third.
/** Wrapper method for calculating Fibonacci numbers
(in RecursiveMethods.java).
pre: n >= 0
@param n The position of the desired Fibonacci number
@return The value of the nth Fibonacci number
*/
public static int fibonacciStart(int n) {
if (n == 0)
return 0;
else
return fibo(1, 0, n);
}
Figure 5.7 traces the execution of the method call fibonacciStart(5). Note that the first arguments for the method calls to fibo form the sequence 1, 1, 2, 3, 5, which is the Fibonacci sequence. Also note that the result of the first return (5) is simply passed on by each successive return. That is because the recursive case does not specify any operations other than returning the result of the next call. Note that the method fibo is an example of tail recursion.
image
FIGURE 5.7 Trace of fibonacciStart(5)
EXERCISES FOR SECTION 5.2
SELF-CHECK
Does the recursive algorithm for raising x to the power n work for negative values of n? Does it work for negative values of x? Indicate what happens if it is called for each of these cases.
Trace the execution of fibonacciStart(5) using activation frames.
Trace the execution of the following using activation frames.
gcd(33, 12)
gcd(12, 33)
gcd(11, 5)
For each of the following method calls, show the argument values in the activation frames that would be pushed onto the run-time stack.
gcd(6, 21)
factorial(5)
gcd(31, 7)
fibonacci(6)
fibonacciStart(7)
See for what value of n the method fibonacci begins to take a long time to run on your computer (over 1 minute). Compare the performance of fibonacciStart and fibo for this same value.
PROGRAMMING
Write a recursive method for raising x to the power n that works for negative n as well as positive n. Use the fact that x−n=1xn
.
Modify the factorial method to throw an IllegalArgumentException if n is negative.
Modify the Fibonacci method to throw an illegal argument exception if its argument is less than or equal to zero.
Write a class that has an iterative method for calculating Fibonacci numbers. Use an array that saves each Fibonacci number as it is calculated. Your method should take advantage of the existence of this array so that subsequent calls to the method simply retrieve the desired Fibonacci number if it has been calculated. If not, start with the largest Fibonacci number in the array rather than repeating all calculations.
5.3 Recursive Array Search
Searching an array is an activity that can be accomplished using recursion. The simplest way to search an array is a linear search. In a linear search, we examine one array element at a time, starting with the first element or the last element, to see whether it matches the target. The array element we are seeking may be anywhere in the array, so on average we will examine n2
items to find the target if it is in the array. If it is not in the array, we will have to examine all n elements (the worst case). This means linear search is an O(n) algorithm.
Design of a Recursive Linear Search Algorithm
Let's consider how we might write a recursive algorithm for an array search that returns the subscript of a target item.
The base case would be an empty array. If the array is empty, the target cannot be there, so the result should be –1. If the array is not empty, we will assume that we can examine just the first element of the array, so another base case would be when the first array element matches the target. If so, the result should be the subscript of the first array element.
The recursive step would be to search the rest of the array, excluding the first element. So our recursive step should search for the target starting with the current second array element, which will become the first element in the next execution of the recursive step. The algorithm follows.
Algorithm for Recursive Linear Array Search
1. if the array is empty
2. The result is –1.
else if the first element matches the target
3. The result is the subscript of the first element.
else
4. Search the array excluding the first element and return the result.
Implementation of Linear Search
The following method, linearSearch (part of class RecursiveMethods), shows the linear search algorithm.
/** Recursive linear search method (in RecursiveMethods.java).
@param items The array being searched
@param target The item being searched for
@param posFirst The position of the current first element
@return The subscript of target if found; otherwise –1
*/
private static int linearSearch(Object[] items,
Object target, int posFirst) {
if (posFirst == items.length)
return –1;
else if (target.equals(items[posFirst]))
return posFirst;
else
return linearSearch(items, target, posFirst + 1);
}
The method parameter posFirst represents the subscript of the current first element. The first condition tests whether the array left to search is empty. The condition (posFirst == items.length) is true when the subscript of the current first element is beyond the bounds of the array. If so, method linearSearch returns –1. The statement
return linearSearch(items, target, posFirst + 1);
implements the recursive step; it increments posFirst to exclude the current first element from the next search.
To search an array x for target, you could use the method call
RecursiveMethods.linearSearch(x, target, 0)
However, since the third argument would always be 0, we can define a nonrecursive wrapper method (also called linearSearch) that has just two parameters: items and target.
/** Wrapper for recursive linear search method (in
RecursiveMethods.java).
@param items The array being searched
@param target The object being searched for
@return The subscript of target if found; otherwise –1
*/
public static int linearSearch(Object[] items, Object target) {
return linearSearch(items, target, 0);
}
The sole purpose of this method is to call the recursive method, passing on its arguments with 0 as a third argument, and return its result. This method definition overloads the previous one, which has private visibility.
Figure 5.8 traces the execution of the call to linearSearch in the second statement.
String[] greetings = {"Hi", "Hello", "Shalom"};
int posHello = linearSearch(greetings, "Hello");
The value returned to posHello will be 1.
image
FIGURE 5.8 Trace of linearSearch(greetings, "Hello")
Design of a Binary Search Algorithm
A second approach to searching an array is called binary search. Binary search can be performed only on an array that has been sorted. In binary search, the stopping cases are the same as for linear search:
When the array is empty.
When the array element being examined matches the target.
However, rather than examining the last array element, binary search compares the “middle” element of the array to the target. If there is a match, it returns the position of the middle element. Otherwise, because the array has been sorted, we know with certainty which half of the array must be searched to find the target. We then can exclude the other half of the array (not just one element as with linear search). The binary search algorithm (first introduced in Section 5.1) follows.
Binary Search Algorithm
1. if the array is empty
2. Return –1 as the search result.
else if the middle element matches the target
3. Return the subscript of the middle element as the result.
else if the target is less than the middle element
4. Recursively search the array elements before the middle element and return the result.
else
5. Recursively search the array elements after the middle element and return the result.
Figure 5.9 illustrates binary search for an array with seven elements. The shaded array elements are the ones that are being searched each time. The array element in bold is the one that is being compared to the target. In the first call, we compare "Dustin" to "Elliot". Because "Dustin" is smaller, we need to search only the part of the array before "Elliot" (consisting of just three candidates). In the second call, we compare "Dustin" to "Debbie". Because "Dustin" is larger, we need to search only the shaded part of the array after "Debbie" (consisting of just one candidate). In the third call, we compare "Dustin" to "Dustin", and the subscript of "Dustin" (2) is our result. If there were no match at this point (e.g., the array contained "Duncan" instead of "Dustin"), the array of candidates to search would become an empty array.
image
FIGURE 5.9 Binary Search for "Dustin"
Efficiency of Binary Search
Because we eliminate at least half of the array elements from consideration with each recursive call, binary search is an O(log n) algorithm. To verify this, an unsuccessful search of an array of size 16 could result in our searching arrays of size 16, 8, 4, 2, and 1 to determine that the target was not present. Thus, an array of size 16 requires a total of 5 probes in the worst case (16 is 24, so 5 is log 216 + 1). If we double the array size, we would need to make only 6 probes for an array of size 32 in the worst case (32 is 25, so 6 is log2 32 + 1). The advantages of binary search become even more apparent for larger arrays. For an array with 32,768 elements, the maximum number of probes required would be 16 (log2 32,768 is 15), and if we expand the array to 65,536 elements, we would increase the number of probes required only to 17.
The Comparable Interface
We introduced the Comparable interface in Section 2.8. Classes that implement this interface must define a compareTo method that enables its objects to be compared in a standard way. The method compareTo returns an integer whose value indicates the relative ordering of the two objects being compared (as described in the @return tag below). If the target is type Comparable, we can apply its compareTo method to compare the target to the objects stored in the array. T represents the type of the object being compared.
/** Instances of classes that realize this interface can be
compared.
@param <T> The type of object this object can be compared to.
*/
public interface Comparable<T> {
/** Method to compare this object to the argument object.
@param obj The argument object
@return Returns a negative integer if this object < obj;
zero if this object equals obj;
a positive integer if this object > obj
*/
int compareTo(T obj);
}
Implementation of Binary Search
Listing 5.1 shows a recursive implementation of the binary search algorithm and its nonrecursive wrapper method. The parameters first and last are the subscripts of the first element and last element in the array being searched. For the initial call to the recursive method from the wrapper method, first is 0 and last is items.length – 1. The parameter target is type Comparable.
The condition (first > last) becomes true when the list of candidates is empty. The statement
int middle = (first + last) / 2;
computes the subscript of the “middle” element in the current array (midway between first and last).
The statement
int compResult = target.compareTo(items[middle]);
saves the result of comparing the target to the middle element of the array. If the result is 0 (a match), the subscript middle is returned. If the result is negative, the recursive step
return binarySearch(items, target, first, middle – 1);
returns the result of searching the part of the current array before the middle item (with subscripts first through middle – 1). If the result is positive, the recursive step
return binarySearch(items, target, middle + 1, last);
returns the result of searching the part of the current array after the middle item (with subscripts middle + 1 through last).
LISTING 5.1
Method binarySearch
/** Recursive binary search method (in RecursiveMethods.java).
@param <T> The item type
@param items The array being searched
@param target The object being searched for
@param first The subscript of the first element
@param last The subscript of the last element
@return The subscript of target if found; otherwise –1.
*/
private static <T> int binarySearch(T[] items, Comparable<T> target,
int first, int last) {
if (first > last)
return –1; // Base case for unsuccessful search.
else {
int middle = (first + last) / 2; // Next probe index.
int compResult = target.compareTo(items[middle]);
if (compResult == 0)
return middle; // Base case for successful search.
else if (compResult < 0)
return binarySearch(items, target, first, middle – 1);
else
return binarySearch(items, target, middle + 1, last);
}
/** Wrapper for recursive binary search method (in RecursiveMethods.java).
@param <T> The item type.
@param items The array being searched
@param target The object being searched for
@return The subscript of target if found; otherwise –1.
*/
public static <T> int binarySearch(T[] items, Comparable<T> target) {
return binarySearch(items, target, 0, items.length – 1);
}
Figure 5.10 traces the execution of binarySearch for the array shown in Figure 5.9. The parameter items always references the same array; however, the pool of candidates changes with each call.
image
FIGURE 5.10 Trace of binarySearch(kidNames, "Dustin")
image SYNTAX Declaring a Generic Method
FORM:
methodModifiers <genericParameters> returnType methodName(methodParameters)
EXAMPLE
public static <T> int binarySearch(T[] items, Comparable<T> target)
MEANING
To declare a generic method, list the genericParameters inside the symbol pair <> and between the methodModifers (e.g., public static) and the returnType. The genericParameters can then be used in the specification of the methodParameters and in the method body.
Testing Binary Search
To test the binary search algorithm, you must test arrays with an even number of elements and arrays with an odd number of elements. You must also test arrays that have duplicate items. Each array must be tested for the following cases:
The target is the element at each position of the array, starting with the first position and ending with the last position.
The target is less than the smallest array element.
The target is greater than the largest array element.
The target is a value between each pair of items in the array.
Method Arrays.binarySearch
The Java API class Arrays contains a binarySearch method. It can be called with sorted arrays of primitive types or with sorted arrays of objects. If the objects in the array are not mutually comparable or if the array is not sorted, the results are undefined. If there are multiple copies of the target value in the array, there is no guarantee as to which one will be found. This is the same as for our binarySearch method. The method throws a ClassCastException if the target is not comparable to the array elements (e.g., if the target is type Integer and the array elements are type String).
EXERCISES FOR SECTION 5.3
SELF-CHECK
1.
For the array shown in Figure 5.9, show the values of first, last, middle, and compResult in successive frames when searching for a target of "Rich"; when searching for a target of "Alice"; and when searching for a target of "Daryn".
How many elements will be compared to target for an unsuccessful binary search in an array of 1000 items? What is the answer for 2000 items?
If there are multiple occurrences of the target item in an array, what can you say about the subscript value that will be returned by linearSearch? Answer the same question for binarySearch.
Write a recursive algorithm to find the largest value in an array of integers.
Write a recursive algorithm that searches a string for a target character and returns the position of its first occurrence if it is present or −1 if it is not.
PROGRAMMING
Write a recursive method to find the sum of all values stored in an array of integers.
Write a recursive linear search method with a recursive step that finds the last occurrence of a target in an array, not the first. You will need to modify the linear search method so that the last element of the array is always tested, not the first. You will need to pass the current length of the array as an argument.
Implement the method for Self-Check Exercise 4. You will need to keep track of the largest value found so far through a method parameter.
Implement the method for Self-Check Exercise 5. You will need to keep track of the current position in the string through a method parameter.
5.4 Recursive Data Structures
Computer scientists often encounter data structures that are defined recursively. A recursive data structure is one that has another version of itself as a component. We will define the tree data structure as a recursive data structure in Chapter 6, but we can also define a linked list, described in Chapter 2, as a recursive data structure. In this section, we demonstrate that recursive methods provide a very natural mechanism for processing recursive data structures. The first language developed for artificial intelligence research was a recursive language designed expressly for LISt Processing and therefore called LISP.
Recursive Definition of a Linked List
The following definition implies that a nonempty linked list is a collection of nodes such that each node references another linked list consisting of the nodes that follow it in the list. The last node references an empty list.
A linked list is empty, or it consists of a node, called the list head, that stores data and a reference to a linked list.
Class LinkedListRec
We will define a class LinkedListRec<E> that implements several list operations using recursive methods. The class LinkedListRec<E> has a private inner class called Node<E>, which is defined in Listing 2.1. A Node<E> object has attributes data (type E) and next (type Node). Class LinkedListRec<E> has a single data field head (data type Node<E>).
/** A recursive linked list class with recursive methods. */
public class LinkedListRec<E> {
/** The list head */
private Node<E> head;
// Insert inner class Node<E> here. See Listing 2.1.
. . .
}
We will write the following recursive methods: size (returns the size), toString (represents the list contents as a string), add (adds an element to the end of the list), and replace (replaces one object in a list with another). We code each operation using a pair of methods: a public wrapper method that calls a private recursive method. To perform a list operation, you apply a wrapper method to an instance of class LinkedListRec.
Method size
The method size returns the size of a linked list and is similar to the method length defined earlier for a string. The recursive method returns 0 if the list is empty (head == null is true). Otherwise, the statement
return 1 + size(head.next);
returns 1 plus the size of the rest of the list that is referenced by head.next.
The wrapper method calls the recursive method, passing the list head as an argument, and returns the value returned by the recursive method. In the initial call to the recursive method, head will reference the first list node. In each subsequent call, head will reference the successor of the node that it currently references.
/** Finds the size of a list.
@param head The head of the current list
@return The size of the current list
*/
private int size(Node<E> head) {
if (head == null)
return 0;
else
return 1 + size(head.next);
}
/** Wrapper method for finding the size of a list.
@return The size of the list
*/
public int size() {
return size(head);
}
Method toString
The method toString returns a string representation of a linked list. The recursive method is very similar to the method size. The statement
return head.data + "\n" + toString(head.next);
appends the data in the current list head to the string representation of the rest of the list. The line space character is inserted after each list item. If the list contains the elements "hat", "55", and "dog", the string result would be "hat\n55\ndog\n".
/** Returns the string representation of a list.
@param head The head of the current list
@return The state of the current list
*/
private String toString(Node<E> head) {
if (head == null)
return "";
else
return head.data + "\n" + toString(head.next);
}
/** Wrapper method for returning the string representation of a list.
@return The string representation of the list
*/
public String toString() {
return toString(head);
}
Method replace
The method replace replaces each occurrence of an object in a list (parameter oldObj) with a different object (parameter newObj). The if statement in the recursive method is different from what we are used to. The method does nothing for the base case of an empty list. If the list is not empty, the if statement
if (oldObj.equals(head.data))
head.data = newObj;
tests whether the item in the current list head matches oldObj. If so, it stores newObj in the current list head. Regardless of whether or not a replacement is performed, the method replace is called recursively to process the rest of the list.
/** Replaces all occurrences of oldObj with newObj.
post: Each occurrence of oldObj has been replaced by newObj.
@param head The head of the current list
@param oldObj The object being removed
@param newObj The object being inserted
*/
private void replace(Node<E> head, E oldObj, E newObj) {
if (head != null) {
if (oldObj.equals(head.data))
head.data = newObj;
replace(head.next, oldObj, newObj);
}
}
/** Wrapper method for replacing oldObj with newObj.
post: Each occurrence of oldObj has been replaced by newObj.
@param oldObj The object being removed
@param newObj The object being inserted
*/
public void replace(E oldObj, E newObj) {
replace(head, oldObj, newObj);
}
Method add
You can use the add method to add nodes to an existing list. You can also use it to build a list by adding new nodes to the end of an initially empty list.
The add methods have two features that are different from what we have seen before. The wrapper method tests for an empty list (head == null is true), and it calls the recursive add method only if the list is not empty. If the list is empty, the wrapper add method creates a new node, which is referenced by the data field head, and stores the first list item in this node.
/** Adds a new node to the end of a list.
@param head The head of the current list
@param data The data for the new node
*/
private void add(Node<E> head, E data) {
// If the list has just one element, add to it.
if (head.next == null)
head.next = new Node<>(data);
else
add(head.next, data); // Add to rest of list.
}
/** Wrapper method for adding a new node to the end of a list.
@param data The data for the new node
*/
public void add(E data) {
if (head == null)
head = new Node<>(data); // List has 1 node.
else
add(head, data);
}
For each node referenced by argument head, the recursive method tests to see whether the node referenced by argument head is the last node in the list (head.next is null). If so, the method add then resets head.next to reference a new node that contains the data being inserted.
image PITFALL
Testing for an Empty List Instead of Testing for the Last List Node
In the recursive method add, we test whether head.next is null. This condition is true when head references a list with just one node. We then reset its next field to reference a new node. If we tested whether head was null (an empty list) and then executed the statement
head = new Node<>(data);
this would have no effect on the original list. The local reference head would be changed to reference the new node, but this node would not be connected to a node in the original list.
Removing a List Node
One of the reasons for using linked lists is that they enable easy insertion and removal of nodes. We show how to do removal next and leave insertion as an exercise. In the following recursive method remove, the first base case returns false if the list is empty. The second base case determines whether the list head should be removed by comparing its data field to outData. If there is a match, the assignment statement removes the list head by connecting its predecessor (referenced by pred) to the successor of the list head. For this case, method remove returns true. The recursive case applies remove to the rest of the list. In the next execution of the recursive method, the current list head will be referenced by pred, and the successor of the current list head will be referenced by head.
/** Removes a node from a list.
post: The first occurrence of outData is removed.
@param head The head of the current list
@param pred The predecessor of the list head
@param outData The data to be removed
@return true if the item is removed
and false otherwise
*/
private boolean remove(Node<E> head, Node<E> pred, E outData) {
if (head == null) // Base case – empty list.
return false;
else if (head.data.equals(outData)) { // 2nd base case.
pred.next = head.next; // Remove head.
return true;
} else
return remove(head.next, head, outData);
}
The following wrapper method takes care of the special case where the node to be removed is at the head of the list. The first condition returns false if the list is empty. The second condition removes the list head and returns true if the list head contains the data to be removed. The else clause calls the recursive remove method. In the first execution of the recursive method, head will reference the actual second node and pred will reference the actual first node.
/** Wrapper method for removing a node (in LinkedListRec).
post: The first occurrence of outData is removed.
@param outData The data to be removed
@return true if the item is removed,
and false otherwise
*/
public boolean remove(E outData) {
if (head == null)
return false;
else if (head.data.equals(outData)) {
head = head.next;
return true;
} else
return remove(head.next, head, outData);
}
EXERCISES FOR SECTION 5.4
SELF-CHECK
Describe the result of executing each of the following statements:
LinkedListRec<String> aList = new LinkedListRec<String>();
aList.add("bye");
aList.add("hello");
System.out.println(aList.size() + ", " + aList.toString());
aList.replace("hello", "welcome");
aList.add("OK");
aList.remove("bye");
aList.remove("hello");
System.out.println(aList.size() + ", " + aList.toString());
Trace each call to a LinkedListRec method in Exercise 1 above.
Write a recursive algorithm for method insert(E obj, int index) where index is the position of the insertion.
Write a recursive algorithm for method remove(int index) where index is the position of the item to be removed.
PROGRAMMING
Write an equals method for the LinkedListRec class that compares this LinkedListRec object to one specified by its argument. Two lists are equal if they have the same number of nodes and store the same information at each node. Don't use the size method.
Write a search method that returns true if its argument is stored as the data field of a LinkedListRec node and returns false if its argument is not stored in any node.
Write a recursive method insertBefore that inserts a specified data object before the first occurrence of another specified data object. For example, the method call aList.insertBefore(target, inData) would insert the object referenced by inData in a new node just before the first node of aList that stores a reference to target as its data.
Write a recursive method reverse that reverses the elements in a linked list.
Code method insert in Self-Check Exercise 3.
Code method remove in Self-Check Exercise 4.
5.5 Problem Solving with Recursion
In this section, we discuss recursive solutions to two problems. Our recursive solutions will break each problem up into multiple smaller versions of the original problem. Both problems are easier to solve using recursion because recursive thinking enables us to split each problem into more manageable subproblems. They would both be much more difficult to solve without recursion.
CASE STUDY Towers of Hanoi
Problem
You may be familiar with a version of this problem that is sold as a child's puzzle. There is a board with three pegs and three disks of different sizes (see Figure 5.11). The goal of the game is to move the three disks from the peg where they have been placed (largest disk on the bottom, smallest disk on the top) to one of the empty pegs, subject to the following constraints:
Only the top disk on a peg can be moved to another peg.
A larger disk cannot be placed on top of a smaller disk.
image
FIGURE 5.11 Children's Version of Towers of Hanoi
Analysis
We can solve this problem by displaying a list of moves to be made. The problem inputs will be the number of disks to move, the starting peg, the destination peg, and the temporary peg. Table 5.1 shows the problem inputs and outputs. We will write a class Tower that contains a method showMoves that builds a string with all the moves.
TABLE 5.1 Inputs and Outputs for Towers of Hanoi Problem
Problem Inputs
Number of disks (an integer)
Letter of starting peg: L (left), M (middle), or R (right)
Letter of destination peg: (L, M, or R), but different from starting peg
Letter of temporary peg: (L, M, or R), but different from starting peg and destination peg
Problem Outputs
A list of moves
Design
We still need to determine a strategy for making a move. If we examine the situation in Figure 5.11 (all three disks on the L peg), we can derive a strategy to solve it. If we can figure out how to move the top two disks to the M peg (a two-disk version of the original problem), we can then place the bottom disk on the R peg (see Figure 5.12). Now all we need to do is move the two disks on the M peg to the R peg. If we can solve both of these two-disk problems, then the three-disk problem is also solved.
image
FIGURE 5.12 Towers of Hanoi After the First Two Steps in Solution of the Three-Disk Problem
Solution to Two-Disk Problem: Move Three Disks from Peg L to Peg R
Move the top two disks from peg L to peg M.
Move the bottom disk from peg L to peg R.
Move the top two disks from peg M to peg R.
We can split the solution to each two-disk problem into three problems involving single disks. We solve the second two-disk problem next; the solution to the first one (move the top two disks from peg L to peg M) is quite similar.
Solution to Two-Disk Problem: Move Top Two Disks from Peg M to Peg R
Move the top disk from peg M to peg L.
Move the bottom disk from peg M to peg R.
Move the top disk from peg L to peg R.
In Figure 5.13, we show the pegs after Steps 1 and 2. When Step 3 is completed, the three pegs will be on peg R.
image
FIGURE 5.13 Towers of Hanoi after First Two Steps in Solution of the Two-Disk Problem
In a similar way, we can split a four-disk problem into two three-disk problems. Figure 5.14 shows the pegs after the top three disks have been moved from peg L to peg M. Because we know how to solve three-disk problems, we can also solve four-disk problems.
image
FIGURE 5.14 Towers of Hanoi after the First Two Steps in Solution of the Four-Disk Problem
Solution to Four-Disk Problem: Move Four Disks from Peg L to Peg R
Move the top three disks from peg L to peg M.
Move the bottom disk from peg L to peg R.
Move the top three disks from peg M to peg R.
Next, we show a general recursive algorithm for moving n disks from one of the three pegs to a different peg.
Recursive Algorithm for n-Disk Problem: Move n Disks from the Starting Peg to the Destination Peg
1. if n is 1
2. Move disk 1 (the smallest disk) from the starting peg to the destination peg.
3. else
4. Move the top n − 1 disks from the starting peg to the temporary peg (neither starting nor destination peg).
5. Move disk n (the disk at the bottom) from the starting peg to the destination peg.
6. Move the top n − 1 disks from the temporary peg to the destination peg.
The stopping case is the one-disk problem. The recursive step enables us to split the n-disk problem into two (n − 1) disk problems and a single-disk problem. Each problem has a different starting peg and destination peg.
Our recursive solution method showMoves will display the solution as a list of disk moves. For each move, we show the number of the disk being moved and its starting and destination pegs. For example, for the two-disk problem shown earlier (move two disks from the middle peg, M, to the right peg, R), the list of moves would be
Move disk 1 from peg M to peg L
Move disk 2 from peg M to peg R
Move disk 1 from peg L to peg R
The method showMoves must have the number of disks, the starting peg, the destination peg, and the temporary peg as its parameters. If there are n disks, the bottom disk has number n (the top disk has number 1). Table 5.2 describes the method required for class TowersOfHanoi.
TABLE 5.2 Class TowersOfHanoi
Method Behavior
public String showMoves(int n, char startPeg, char destPeg, char tempPeg) Builds a string containing all moves for a game with n disks on startPeg that will be moved to destPeg using
tempPeg for temporary storage of disks being moved
Implementation
Listing 5.2 shows class TowersOfHanoi. In method showMoves, the recursive step
return showMoves(n – 1, startPeg, tempPeg, destPeg)
+ "Move disk " + n + " from peg " + startPeg
+ " to peg " + destPeg + "\n”
+ showMoves(n – 1, tempPeg, destPeg, startPeg);
returns the string formed by concatenating the list of moves for the first (n – 1)-disk problem (the recursive call after return), the move required for the bottom disk (disk n), and the list of moves for the second (n – 1)-disk problem.
LISTING 5.2
Class TowersOfHanoi
/** Class that solves Towers of Hanoi problem. */
public class TowersOfHanoi {
/** Recursive method for "moving" disks.
pre: startPeg, destPeg, tempPeg are different.
@param n is the number of disks
@param startPeg is the starting peg
@param destPeg is the destination peg
@param tempPeg is the temporary peg
@return A string with all the required disk moves
*/
public static String showMoves(int n, char startPeg,
char destPeg, char tempPeg) {
if (n == 1) {
return "Move disk 1 from peg " + startPeg +
" to peg " + destPeg + "\n";
} else { // Recursive step
return showMoves(n – 1, startPeg, tempPeg, destPeg)
+ "Move disk " + n + " from peg " + startPeg
+ " to peg " + destPeg + "\n"
+ showMoves(n – 1, tempPeg, destPeg, startPeg);
}
}
Testing
Figure Figure 5.15 shows the result of executing the following main method for the data 3, L, and R (“move 3 disks from peg L to peg R”). The first three lines are the solution to the problem “move 2 disks from peg L to peg M,” and the last three lines are the solution to the problem “move 2 disks from peg M to peg R.”
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
System.out.print("Enter number of disks ");
int nDisks = in.nextInt();
String moves = showMoves(nDisks, 'L', 'R', 'M');
System.out.println(moves);
}
image
FIGURE 5.15 Solution to “Move 3 Disks from Peg L to Peg R”
Visualization of Towers of Hanoi
We have provided a graphical visualization that you can use to observe the movement of disks in a solution to the Towers of Hanoi. You can access it through the textbook Web site for this book.
CASE STUDY Counting Cells in a Blob
In this case study, we consider how we might process an image that is presented as a two-dimensional array of color values. The information in the two-dimensional array might come from a variety of sources. For example, it could be an image of part of a person's body that comes from an X-ray or an MRI, or it could be a picture of part of the earth's surface taken by a satellite. Our goal in this case study is to determine the size of any area in the image that is considered abnormal because of its color values.
Problem
You have a two-dimensional grid of cells, and each cell contains either a normal background color or a second color, which indicates the presence of an abnormality. The user wants to know the size of a blob, where a blob is a collection of contiguous abnormal cells. The user will enter the x, y coordinates of a cell in the blob, and the count of all cells in that blob will be determined.
Analysis
Data Requirements
PROBLEM INPUTS
The two-dimensional grid of cells
The coordinates of a cell in a blob
PROBLEM OUTPUTS
The count of cells in the blob
Classes
We will have two classes. Class TwoDimGrid will manage the two-dimensional grid of cells. You can find the discussion of the design and implementation of this class on the Web site for this book. Here we will focus on the design of class Blob, which contains the recursive method that counts the number of cells in a blob.
Design
Table 5.3 describes the public methods of class TwoDimGrid, and Table 5.4 describes class Blob.
TABLE 5.3 Class TwoDimGrid
Method Behavior
void recolor(int x, int y, Color aColor) Resets the color of the cell at position (x, y) to aColor
Color getColor(int x, int y) Retrieves the color of the cell at position (x, y)
int getNRows() Returns the number of cells in the y-axis
int getNCols() Returns the number of cells in the x-axis
TABLE 5.4 Class Blob
Method Behavior
int countCells(int x, int y) Returns the number of cells in the blob at (x, y)
Method countCells in class Blob is a recursive method that is applied to a TwoDimGrid object. Its parameters are the (x, y) position of a cell. The algorithm follows.
Algorithm for countCells(x, y)
1. if the cell at (x, y) is outside the grid
2. The result is 0.
else if the color of the cell at (x, y) is not the abnormal color
3. The result is 0.
else
4. Set the color of the cell at (x, y) to a temporary color.
5. The result is 1 plus the number of cells in each piece of the blob that includes a nearest neighbor.
The two stopping cases are reached if the coordinates of the cell are out of bounds or if the cell does not have the abnormal color and, therefore, can't be part of a blob. The recursive step involves counting 1 for a cell that has the abnormal color and adding the counts for the blobs that include each immediate neighbor cell. Each cell has eight immediate neighbors: two in the horizontal direction, two in the vertical direction, and four in the diagonal directions.
If no neighbor has the abnormal color, then the result will be just 1. If any neighbor cell has the abnormal color, then it will be counted along with all its neighbor cells that have the abnormal color, and so on until no neighboring cells with abnormal color are encountered (or the edge of the grid is reached). The reason for setting the color of the cell at (x, y) to a temporary color is to prevent it from being counted again when its neighbors’ blobs are counted.
ImplementationListing
Listing 5.3 shows class Blob. The interface GridColors defines the three constants: BACKGROUND, ABNORMAL, and TEMPORARY. We make these constants available by using the static import statement:
import static GridColors.*;
The first terminating condition,
(x < 0 || x >= grid.getNCols() || y < 0 || y >= grid.getNRows())
compares x to 0 and the value returned by getNCols(), the number of columns in the grid. Because x is plotted along the horizontal axis, it is compared to the number of columns, not the number of rows. The same test is applied to y and the number of rows. The second terminating condition,
(!grid.getColor(x, y).equals(ABNORMAL))
is true if the cell at (x, y) has either the background color or the temporary color.
The recursive step is implemented by the statement
return 1
+ countCells(x – 1, y + 1) + countCells(x, y + 1)
+ countCells(x + 1, y + 1) + countCells(x – 1, y)
+ countCells(x + 1, y) + countCells(x – 1, y – 1)
+ countCells(x, y – 1) + countCells(x + 1, y – 1);
Each recursive call to countCells has as its arguments the coordinates of a neighbor of the cell at (x, y). The value returned by each call will be the number of cells in the blob it belongs to, excluding the cell at (x, y) and any other cells that may have been counted already.
LISTING 5.3
Class Blob
import java.awt.*;
import static GridColors.*;
/** Class that solves problem of counting abnormal cells. */
public class Blob {
/** The grid */
private TwoDimGrid grid;
/** Constructors */
public Blob(TwoDimGrid grid) {
this.grid = grid;
}
/** Finds the number of cells in the blob at (x,y).
pre: Abnormal cells are in ABNORMAL color;
Other cells are in BACKGROUND color.
post: All cells in the blob are in the TEMPORARY color.
@param x The x-coordinate of a blob cell
@param y The y-coordinate of a blob cell
@return The number of cells in the blob that contains (x, y)
*/
public int countCells(int x, int y) {
int result;
if (x < 0 || x >= grid.getNCols()
|| y < 0 || y >= grid.getNRows())
return 0;
else if (!grid.getColor(x, y).equals(ABNORMAL))
return 0;
else {
grid.recolor(x, y, TEMPORARY);
return 1
+ countCells(x – 1, y + 1) + countCells(x, y + 1)
+ countCells(x + 1, y + 1) + countCells(x – 1, y)
+ countCells(x + 1, y) + countCells(x – 1, y – 1)
+ countCells(x, y – 1) + countCells(x + 1, y – 1);
}
}
}
image SYNTAX Static Import
FORM:
import static Class.*;
or
import static Class.StaticMember;
EXAMPLE:
import static GridColors.*;
MEANING:
The static members of the class Class or interface Class are visible in the file containing the import. If * is specified, then all static members are imported, otherwise if a specific member is listed, then this member is visible.
Testing
To test the recursive algorithm in this case study and the one in the next section, we will need to implement class TwoDimGrid. To make the program interactive and easy to use, we implemented TwoDimGrid as a two-dimensional grid of buttons placed in a panel. When the button panel is placed in a frame and displayed, the user can toggle the color of a button (from normal to abnormal and back to normal) by clicking it. Similarly, the program can change the color of a button by applying the recolor method to the button. Information about the design of class TwoDimGrid is on the textbook Web site for this book, as is the class itself.
We also provide a class BlobTest on the textbook Web site. This class allows the user to load the colors for the button panel from a file that contains a representation of the image as lines of 0s and 1s, where 0 is the background color and 1 is the abnormal color. Alternatively, the user can set the dimensions of the grid and then enter the abnormal cells by clicking on each button that represents an abnormal cell. When the grid has been finalized, the user clicks twice on one of the abnormal cells (to change its color to normal and then back to abnormal) and then clicks the button labeled Solve. This invokes method countCells with the coordinates of the last button clicked as its arguments. Figure 5.16 shows a sample grid of buttons with the x, y coordinate of each button shown as the button label. The background cells are dark gray, and the abnormal cells are light gray. Invoking countCells with a starting point of (x = 4, y = 1) should return a count of 7. Figure 5.17 shows the blob cells in the temporary color (black) after the execution of method countCells.
image
FIGURE 5.16 A Sample Grid for Counting Cells in a Blob
image
FIGURE 5.17 Blob Cells (in Black) after Execution of countCells
When you test this program, make sure you verify that it works for the following cases:
A starting cell that is on the edge of the grid.
A starting cell that has no neighboring abnormal cells.
A starting cell whose only abnormal neighbor cells are diagonally connected to it.
A “bull's-eye”: a starting cell whose neighbors are all normal but their neighbors are abnormal.
A starting cell that is normal.
A grid that contains all abnormal cells.
A grid that contains all normal cells.
EXERCISES FOR SECTION 5.5
SELF-CHECK
What is the big-O for the Towers of Hanoi as a function of n, where n represents the number of disks? Compare it to the function 2n.
How many moves would be required to solve the five-disk problem?
Provide a “trace” of the solution to a four-disk problem by showing all the calls to showMoves that would be generated.
Explain why the first condition of method countCells must precede the second condition.
PROGRAMMING
Modify method countCells, assuming that cells must have a common side in order to be counted in the same blob. This means that they must be connected horizontally or vertically but not diagonally. Under this condition, the value of the method call aBlob.countCells(4, 1) would be 4 for the grid in Figure 5.16.
Write a method Blob.restore that restores the grid to its original state. You will need to reset the color of each cell that is in the temporary color back to its original color.
5.6 Backtracking
In this section, we consider the problem-solving technique called backtracking. Backtracking is an approach to implementing systematic trial and error in a search for a solution. An application of backtracking is finding a path through a maze.
If you are attempting to walk through a maze, you will probably follow the general approach of walking down a path as far as you can go. Eventually either you will reach your destination and exit the maze, or you won't be able to go any further. If you exit the maze, you are done. Otherwise, you need to retrace your steps (backtrack) until you reach a fork in the path. At each fork, if there is a branch you did not follow, you will follow that branch hoping to reach your destination. If not, you will retrace your steps again, and so on.
What makes backtracking different from random trial and error is that backtracking provides a systematic approach to trying alternative paths and eliminating them if they don't work out. You will never try the exact same path more than once, and you will eventually find a solution path if one exists.
Problems that are solved by backtracking can be described as a set of choices made by some method. If, at some point, it turns out that a solution is not possible with the current set of choices, the most recent choice is identified and removed. If there is an untried alternative choice, it is added to the set of choices and search continues. If there is no untried alternative choice, then the next most recent choice is removed and an alternative is sought for it. This process continues until either we reach a choice with an untried alternative and can continue our search for a solution, or we determine that there are no more alternative choices to try. Recursion allows us to implement backtracking in a relatively straightforward manner because we can use each activation frame to remember the choice that was made at that particular decision point.
We will show how to use backtracking to find a path through a maze, but it can be applied to many other kinds of problems that involve a search for a solution. For example, a program that plays chess may use a kind of backtracking. If a sequence of moves it is considering does not lead to a favorable position, it will backtrack and try another sequence.
CASE STUDY Finding a Path through a Maze
Problem
Use backtracking to find and display the path through a maze. From each point in a maze, you can move to the next cell in the horizontal or vertical direction, if that cell is not blocked. So there are at most four possible moves from each point.
Analysis
Our maze will consist of a grid of colored cells like the grid used in the previous case study. The starting point is the cell at the top left corner (0, 0), and the exit point is the cell at the bottom right corner (getNCols() – 1, getNRows() – 1). All cells that can be part of a path will be in the BACKGROUND color. All cells that represent barriers and cannot be part of a path will be in the ABNORMAL color. To keep track of a cell that we have visited, we will set it to the TEMPORARY color. If we find a path, all cells on the path will be reset to the PATH color (a new color for a button defined in GridColors). So there are a total of four possible colors for a cell.
Design
The following recursive algorithm returns true if a path is found. It changes the color of all cells that are visited but found not to be on the path to the temporary color. In the recursive algorithm, each cell (x, y) being tested is reachable from the starting point. We can use recursion to simplify the problem of finding a path from cell (x, y) to the exit. We know that we can reach any unblocked neighbor cell that is in the horizontal or vertical direction from cell (x, y). So a path exists from cell (x, y) to the maze exit if there is a path from a neighbor cell of (x, y) to the maze exit. If there is no path from any neighbor cell, we must backtrack and replace (x, y) with an alternative that has not yet been tried. That is done automatically through recursion. If there is a path, it will eventually be found and findMazePath will return true.
Recursive Algorithm for findMazePath(x, y)
1. if the current cell is outside the maze
2. Return false (you are out of bounds).
else if the current cell is part of the barrier or has already been visited
3. Return false (you are off the path or in a cycle).
else if the current cell is the maze exit
4. Recolor it to the path color and return true (you have successfully completed the maze).
else // Try to find a path from the current path to the exit:
5. Mark the current cell as on the path by recoloring it to the path color.
6. for each neighbor of the current cell
7. if a path exists from the neighbor to the maze exit
8. Return true.
// No neighbor of the current cell is on the path.
9. Recolor the current cell to the temporary color (visited) and return false.
If no stopping case is reached (Steps 2, 3, or 4), the recursive case (the else clause) marks the current cell as being on the path and then tests whether there is a path from any neighbor of the current cell to the exit. If a path is found, we return true and begin unwinding from the recursion. During the process of unwinding from the recursion, the method will continue to return true. However, if all neighbors of the current cell are tested without finding a path, this means that the current cell cannot be on the path, so we recolor it to the temporary color and return false (Step 9). Next, we backtrack to a previous call and try to find a path through a cell that is an alternative to the cell just tested. The cell just tested will have been marked as visited (the temporary color), so we won't try using it again.
Note that there is no attempt to find the shortest path through the maze. We just show the first path that is found.
Implementation
Listing 5.4 shows class Maze with data field maze (type TwoDimGrid). There is a wrapper method that calls recursive method findMazePath with its argument values set to the coordinates of the starting point (0, 0). The wrapper method returns the result of this call (true or false).
The recursive version of findMazePath begins with three stopping cases: two unsuccessful and one successful [(x, y) is the exit point]. The recursive case contains an if condition with four recursive calls. Because of short-circuit evaluation, if any call returns true, the rest are not executed. The arguments for each call are the coordinates of a neighbor cell. If a path exists from a neighbor to the maze exit, then the neighbor is part of the solution path, so we return true. If a neighbor cell is not on the solution path, we try the next neighbor until all four neighbors have been tested. If there is no path from any neighbor, we recolor the current cell to the temporary color and return false.
LISTING 5.4
Class Maze
import java.awt.*;
import static GridColors.*;
/** Class that solves maze problems with backtracking. */
public class Maze {
/** The maze */
private TwoDimGrid maze;
public Maze(TwoDimGrid m) {
maze = m;
}
/** Wrapper method. */
public boolean findMazePath() {
return findMazePath(0, 0); // (0, 0) is the start point.
}
/** Attempts to find a path through point (x, y).
pre: Possible path cells are in BACKGROUND color;
barrier cells are in ABNORMAL color.
post: If a path is found, all cells on it are set to the
PATH color; all cells that were visited but are
not on the path are in the TEMPORARY color.
@param x The x-coordinate of current point
@param y The y-coordinate of current point
@return If a path through (x, y) is found, true;
otherwise, false
*/
public boolean findMazePath(int x, int y) {
if (x < 0 || y < 0
|| x >= maze.getNCols() || y >= maze.getNRows())
return false; // Cell is out of bounds.
else if (!maze.getColor(x, y).equals(BACKGROUND))
return false; // Cell is on barrier or dead end.
else if (x == maze.getNCols() – 1
&& y == maze.getNRows() – 1) {
maze.recolor(x, y, PATH); // Cell is on path
return true; // and is maze exit.
} else { // Recursive case.
// Attempt to find a path from each neighbor.
// Tentatively mark cell as on path.
maze.recolor(x, y, PATH);
if (findMazePath(x – 1, y)
|| findMazePath(x + 1, y)
|| findMazePath(x, y – 1)
|| findMazePath(x, y + 1 ) ) {
return true;
} else {
maze.recolor(x, y, TEMPORARY); // Dead end.
return false;
}
}
}
}
The Effect of Marking a Cell as Visited
If a path can't be found from a neighbor of the current cell to the maze exit, the current cell is considered a “dead end” and is recolored to the temporary color. You may be wondering whether the program would still work if we just recolored it to the background color. The answer is “yes.” In this case, cells that turned out to be dead ends or cells that were not visited would be in the background color after the program terminated. This would not affect the ability of the algorithm to find a path or to determine that none exists; however, it would affect the algorithm's efficiency. After backtracking, the method could try to place on the path a cell that had been found to be a dead end. The cell would be classified once again as a dead end. Marking it as a dead end (color TEMPORARY) the first time prevents this from happening.
To demonstrate the efficiency of this approach, we tested the program on a maze with four rows and six columns that had a single barrier cell at the maze exit. When we recolored each dead end cell in the TEMPORARY color, it took 93 recursive calls to findMazePath to determine that a path did not exist. When we recolored each tested cell in the BACKGROUND color, it took 177,313 recursive calls to determine that a path did not exist.
Testing
We will use class TwoDimGrid and class MazeTest (from the textbook Web site) to test the maze. The MazeTest class is very similar to BlobTest. The main method prompts for the grid dimensions and creates a new TwoDimGrid object with those dimensions. The class constructor builds the graphical user interface (GUI) for the maze solver, including the button panel, and registers a listener for each button. When the SOLVE button is clicked, method MazeTest.actionPerformed calls findMazePath and displays its result. Figure 5.18 shows the GUI before the SOLVE button is clicked (barrier cells are in light gray, and other cells are in dark gray), and Figure 5.19 shows it after the SOLVE button is clicked and the final path is displayed. In Figure 5.19, the barrier cells are in light gray (ABNORMAL color), the cells on the final path are in white (PATH color), and the cells that were visited but then rejected (not on the path) are in black (TEMPORARY color).
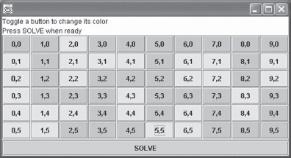
FIGURE 5.18 Maze as Grid of Buttons before SOLVE Is Clicked
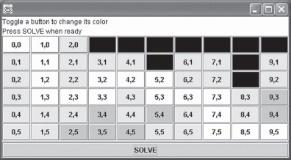
FIGURE 5.19 Maze as Grid of Buttons after SOLVE Is Clicked
You should test this with a variety of mazes, some that can be solved and some that can't (no path exists). You should also try a maze that has no barrier cells and one that has a single barrier cell at the exit point. In the latter case, no path exists.
EXERCISES FOR SECTION 5.6
SELF-CHECK
The terminating conditions in findMazePath must be performed in the order specified. What could happen if the second or third condition was evaluated before the first? If the third condition was evaluated before the second condition?
Does it matter in which order the neighbor cells are tested in findMazePath? How could this order affect the path that is found?
Is the path shown in Figure 5.19 the shortest path to the exit? If not, list the cells on the shortest path.
PROGRAMMING
Show the interface GridColors.
Write a Maze.resetTemp method that recolors the cells that are in the TEMPORARY color to the BACKGROUND color.
Write a Maze.restore method that restores the maze to its initial state.
Chapter Review
A recursive method has the following form, where Step 2 is the base case, and Steps 3 and 4 are the recursive case:
1. if the problem can be solved for the current value of n
2. Solve it.
else
3. Recursively apply the algorithm to one or more problems involvingsmaller values of n.
4. Combine the solutions to the smaller problems to get the solution to the original.
To prove that a recursive algorithm is correct, you must
—Verify that the base case is recognized and solved correctly.
—Verify that each recursive case makes progress toward the base case.
—Verify that if all smaller problems are solved correctly, then the original problem must also be solved correctly.
The run-time stack uses activation frames to keep track of argument values and return points during recursive method calls. Activation frames can be used to trace the execution of a sequence of recursive method calls.
Mathematical sequences and formulas that are defined recursively can be implemented naturally as recursive methods.
Recursive data structures are data structures that have a component that is the same data structure. A linked list can be considered a recursive data structure because each node consists of a data field and a reference to a linked list. Recursion can make it easier to write methods that process a linked list.
Two problems that can be solved using recursion were investigated: the Towers of Hanoi problem and counting cells in a blob.
Backtracking is a technique that enables you to write programs that can be used to explore different alternative paths in a search for a solution.
User-Defined Classes in This Chapter
Blob MazeTest
BlobTest RecursiveMethods
GridColors TowersOfHanoi
LinkedListRec TwoDimGrid
Maze
Quick-Check Exercises
A recursive method has two cases: _________ and _________.
Each recursive call of a recursive method must lead to a situation that is _______ to the __________ case.
The control statement used in a recursive method is the _________ statement.
What three things are stored in an activation frame? Where are the activation frames stored?
You can sometimes substitute _______ for recursion.
Explain how a recursive method might cause a stack overflow exception.
If you have a recursive method and an iterative method that calculate the same result, which do you think would be more efficient? Explain your answer.
Binary search is an O(___) algorithm and linear search is an O(_____) algorithm.
Towers of Hanoi is an O(_____) algorithm. Explain your answer.
Why did you need to provide a wrapper method for recursive methods linearSearch and binarySearch?
Why did you need to provide a wrapper method for recursive methods in the LinkedListRec class?
Review Questions
1. Explain the use of the run-time stack and activation frames in processing recursive method calls.
2. What is a recursive data structure? Give an example.
3. For class LinkedListRec, write a recursive search method that returns true if its target argument is found and false otherwise. If you need a wrapper method, provide one.
4. For class LinkedListRec, write a recursive replaceFirst method that replaces the first occurrence of a reference to its first argument with a reference to its second argument. If you need a wrapper method, provide one.
5. For Towers of Hanoi, show the output string that would be created by the method call showMoves(3, 'R', 'M', 'L'). Also, show the sequence of method calls.
6. For the counting cells in a blob problem, show the activation frames in the first 10 recursive calls to countCells following countCells(4, 1).
7. For the maze path found in Figure 5.19, explain why cells (3, 4), (2, 5), (3, 5), and (4, 5) were never visited and why cells (5, 1) and (3, 0) through (9, 0) were visited and rejected. Show the activation frames for the first 10 recursive calls in solving the maze.
Programming Projects
Download and run class BlobTest. Try running it with a data file made up of lines consisting of 0s and 1s with no spaces between them. Also run it without a data file.
Download and run class MazeTest. Try running it with a data file made up of lines consisting of 0s and 1s with no spaces between them. Also run it without a data file.
Write a recursive method that converts a decimal integer to a binary string. Write a recursive method that converts a binary string to a decimal integer.
Write a LinkedListRec class that has the following methods: size, empty, insertBefore, insertAfter, addAtHead, addAtEnd, remove, replace, peekFront, peekEnd, removeFront, removeEnd, toString. Use recursion to implement most of these methods.
As discussed in Chapter 3, a palindrome is a word that reads the same left to right as right to left. Write a recursive method that determines whether its argument string is a palindrome.
Write a program that will read a list of numbers and a desired sum, then determine the subset of numbers in the list that yield that sum if such a subset exists.
Write a recursive method that will dispense change for a given amount of money. The method will display all combinations of quarters, dimes, nickels, and pennies that equal the desired amount.
Produce the Sierpinski fractal. Start by drawing an equilateral triangle that faces upward. Then draw an equilateral triangle inside it that faces downward.
image
Continue this process on each of the four smaller triangles. Stop when the side dimension for a triangle to be drawn is smaller than a specified minimum size.
Write a recursive method for placing eight queens on a chessboard. The eight queens should be placed so that no queen can capture another. Recall that a queen can move in the horizontal, vertical, or diagonal direction.
Write a recursive method that will find and list all of the one-element sequences of a letters in a char[] array, then all the two-element sequences, then all of the three element sequences, and so on such that the characters in each sequence appear in the same order as they are in the array. For example, for the following array:
char[] letters = {'A', 'C', 'E', 'G'};
the one-element sequences are "A", "C", "E", and "G"
the two-element sequences are "AC", "AE", "AG", "CE", "CG", "EG"
the three-element sequences are "ACE", "ACG", "AEG", and "CEG"
the four-element sequence is "ACEG"
One method of solving a continuous numerical function for a root implements a technique similar to the binary search. Given a numerical function, defined as f(x), and two values of x that are known to bracket one of the roots, an approximation to this root can be determined through a method of repeated division of this bracket. For a set of values of x to bracket a root, the value of the function for one x must be negative and the other must be positive as illustrated below, which plots f(x) for values of x between x1 and x2.
The algorithm requires that the midpoint between x1 and x2 be evaluated in the function, and if it equals zero the root is found; otherwise, x1 or x2 is set to this midpoint. To determine whether to replace x1 or x2, the sign of the midpoint is compared against the signs of the values f(x1) and f(x2). The midpoint replaces the x (x1 or x2) whose function value has the same sign as the function value at the midpoint.
image
This algorithm can be written recursively. The terminating conditions are true when either the midpoint evaluated in the function is zero or the absolute value of x1 – x2 is less than some small predetermined value (e.g., 0.0005). If the second condition occurs, then the root is said to be approximately equal to the last midpoint.
We can use a merge technique to sort two arrays. The mergesort begins by taking adjacent pairs of array values and ordering the values in each pair. It then forms groups of four elements by merging adjacent pairs (first pair with second pair, third pair with fourth pair, etc.) into another array. It then takes adjacent groups of four elements from this new array and merges them back into the original array as groups of eight, and so on. The process terminates when a single group is formed that has the same number of elements as the array. The mergesort is illustrated here for an array with eight elements. Write a mergeSort method.
image
Answers to Quick-Check Exercises
A recursive method has two cases: base case and recursive case.
Each recursive call of a recursive method must lead to a situation that is closer to the base case.
The control statement used in a recursive method is the if statement.
An activation frame stores the following information on the run-time stack: the method argument values, the method local variable values, and the address of the return point in the caller of the method.
You can sometimes substitute iteration for recursion.
A recursive method that doesn't stop would continue to call itself, eventually pushing so many activation frames onto the run-time stack that a stack overflow exception would occur.
An iterative method would generally be more efficient because there is more overhead associated with multiple method calls.
Binary search is an O(log2 n) algorithm and linear search is an O(n) algorithm.
Towers of Hanoi is an O(2n) algorithm because each problem splits into two problems at the next lower level.
Both search methods should be called with the array name and target as arguments. However, the recursive linear search method needs the subscript of the element to be compared to the target. The binary search method needs the search array bounds.
The wrapper method should be applied to a LinkedListRec object. The recursive method needs the current list head as an argument.
Notes
1 Analogy suggested by Rich Pattis, University of California, Irvine, CA.



