Due 7/21/17 @ (2100) Greenwich mean time
Answer these questions:
(a) How does the ALU know which function to perform?
(b) Explain clearly how the fetch-decode-execute cycle works. (What are its steps? Explain each step)
(c) Why is it that if MARIE has 4K words of main memory, addresses must have 12 bits?
(d) What is an opcode?
(e) Explain the functions of all of MARIE's registers.
(f) Explain each step the the MARIE instruction STORE performs.
(g) Describe how an interrupt works and name four different types.
Answer exercise 13 on page 283.
A digital computer has a memory unit with 24 bits per word. The instructions set consists of 150 different operations. All instructions have an operation code part (opcode) and an address part (allowing for only one address). Each instruction is stored in one word memory.
a) how many bits are needed for the opcode?
b) how many bits are left for the address part of the instruction?
c) what is the maximum allowable size for memory?
d) what is the largest unsigned binary number that can be accommodated in one word memory?
Answer exercise 14 on page 283.
A digital computer has a memory unit with 32 bits per word. The instruction set consists of 110 different operations. All instructions have an operation code part (opcode) and two address fields: one for a memory address and one for a register address. This particular system includes eight general-purpose, user-addressable registers. Registers may be loaded directly from memory and memory may be updated directly from the registers. Direct memory-to-memory data movement operations are not supported. Each instruction is stored in one word of memory.
a) how many bits are needed for the opcode?
b) how many bits are needed to specify the register?
c) how many bits are left for the memory address part of the instruction?
d) what is the maximum allowable size for memory?
e) what is the largest unsigned binary number that can be accommodated in one word of memory?
Answer exercise 24 on page 285.
Consider the MARIE program below.
a) list the hexadecimal code for each instruction.
b) draw the symbol table.
c) what is the value stored in the AC when the program terminates?
hex address label instructions
100 start, LOAD A
101 ADD B
102 STORE D
103 CLEAR
104 OUTPUT
105 ADDI D
106 STORE B
107 HALT
108 A, HEX 00FC
109 B, 14-Dec
10A C, HEX 0108
10B D, HEX 0000
Answer exercise 25 on page 285
Consider the MARIE program below.
a) list the hexadecimal code for each instruction.
b) draw the symbol table.
c) what is the value stored in the AC when the program terminates?
hex address label instructions
200 begin, LOAD base
201 ADD Offs
202 loop, SUBT One
203 STORE Addr
204 SKIPCOND 800
205 JUMP Done
206 JUMPI Addr
207 CLEAR
208 done, HALT
209 base, HEX 200
20A Offs, 9-Dec
20B One, HEX 0001
20C Addr, HEX 0000
Answer exercise 29 on page 286.
Write the following code segment in MARIE’s assembly language:
If x>1 then
Y=x+x;
X=0;
Endif;
Y=y+1;
Answer exercise 30 on page 286.
If x<=y then
Y=y+1;
Else if x !=z
Then y=y-1;
Else z=z+1;
Answer Exercises 2 a&b on page 189
For guidance, look at Exercises 1 a & B and their solutions on page 835.
SHOW YOUR INTERMEDIATE COLUMNS that lead you to the final column solution.
Construct a truth table for:
xyz + x(yz)’ + x’(y + z) + (xyz)’
Solution Using Boolean Identities
DeMorgan’s Law: = xyz +x (y’+z’) + x’(y + z) + (xyz)’
Distributive Law: = xyz +x (y’+z’) + (x’y) + (x’z) + (xyz)’
DeMorgan’s Law: = xyz +x (y’+z’) + (x’y) + (x’z) +x’+y’+z’
Distributive Law: = xyz +xy’+xz’+ (x’y) + (x’z) + x’+y’+z’
Distributive Law: = xyz +xy’ (z+z’) +xz’ (y+y’) +x’y (z+z’) +x’z (y+y’)
+ x’ (y+y’) (z+z’) +y’ (x+x’) (z+z’) +z’ (x+x’) (y+y’)
Idempotent Law: = xyz + xy’z + xy’z’ + xz’y + xy’z’ + x’yz + x’yz’
+ x’yz + x’y’z + x’yz + x’yz’ + x’y’z + x’y’z’ + xy’z
+ xy’z’ + x’yz + x’y’z + xyz’ + xy’z’+ x’yz’ + x’y’z’
After removing Idempotent elements:
= xyz + xy’z + xy’z’ + xyz’ + x’yz + x’yz’ + x’y’z + x’y’z’
Note: x=1, y=1, z=1, x’=0, y’=0, z’=0
Therefore:
= xyz + xy’z + xy’z’ + xyz’ + x’yz + x’yz’ + x’y’z + x’y’z’
111 10 1 10 0 110 0 11 0 10 0 0 1 0 0 0
| x | y | z | xyz + x(yz)’ + x’(y + z) + (xyz)’ |
| 1 | |||
| 1 | |||
| 1 | |||
| 1 | |||
| 1 | |||
| 1 | |||
| 1 | |||
| 1 |
b) (x + y’) (x’ + z’) (y’ + z’)
Solution Using Truth Table
| x | y | z | x’ | y’ | z’ | (x + y’) | (x’ + z’) | (y’ + z’) | Product = (x + y’) (x’ + z’) (y’ + z’) |
| 1 | |||||||||
| 1 | |||||||||
| 0 | |||||||||
| 0 | |||||||||
| 1 | |||||||||
| 0 | |||||||||
| 1 | |||||||||
| 0 |
Answer Exercise 9 on page 190
Is the fallowing true or false? Prove your answer.
(x XOR y)’ = xy + (x + y)’
Note:
When adding:
0+0=0
0+1=1
1+0=1
1+1=1
When Multiplying:
0*0=0
0*1=0
1*0=0
1*1=1
Drawing truth table for x XOR y
| x | y | (x XOR y) | (x XOR y)’ |
| 1 | |||
| 0 | |||
| 0 | |||
| 1 |
Drawing truth table for xy + (x + y)’
| x | y | xy | (x + y) | (x + y)’ | xy + (x + y)’ |
| 1 | |||||
| 0 | |||||
| 0 | |||||
| 1 |
Therefore: (x XOR y)’ = xy + (x + y)’ since the truth table for both produces same results
Answer Exercises 10 a and b on page 190.
Show that x = xy + xy’
using truth tables
| x | y | y’ | xy | xy’ | xy + xy’ |
| 0 | |||||
| 0 | |||||
| 1 | |||||
| 1 |
Since x = 0,0,1,1 and xy + xy’= 0,0,1,1 it is true that x = xy + xy’
b) Using Boolean identities
Given: x = xy + xy’
Distributive Law: x = x (y + y’)
Inverse: x = x (1)
Therefore: x=x
Answer Exercise 12 part a on page 190. (Note: Not part b.)
Show that xz = (x + y) (x + y’) (x’ + z)
a) Using truth tables
| x | y | z | x’ | y’ | xz | (x + y) | (x + y’) | (x’ + z) | (x + y)(x + y’)(x’ + z) |
| 0 | 0 | ||||||||
| 0 | 0 | ||||||||
| 0 | 0 | ||||||||
| 0 | 0 | ||||||||
| 0 | 0 | ||||||||
| 1 | 1 | ||||||||
| 0 | 0 | ||||||||
| 1 | 1 |
xz = (x + y)(x + y’)(x’ + z) as seen from same result for xz and (x + y)(x + y’)(x’ + z) columns.
b) Using Boolean identities
xz = (x + y)(x + y’)(x’ + z) :Given
xz = x(y+y’) (x’+z) : Distributive Law (x + y)(x + y’) = x(y+y’)
xz = x(1) (x’+z) : Inverse Law (y+y’) = 1
xz = x(x’+z) : Identity Law (x*1)=x
xz= xx’ + xz : Distributive Law (x(x’+z) = xx’+xz
xz= 0 + xz : Inverse Law xx’ = 0
xz = xz :Therefore xz = (x + y)(x + y’)(x’ + z)
Answer exercise 13 on page 190.
Use any method to prove the fallowing either true or false.
xz + x’y’ + y’z’ = xz + y’
Solution using Truth Table
| x | y | z | x’ | y’ | z’ | xz | x’y’ | y’z’ | xz + x’y’ + y’z’ | xz + y’ |
| 1 | 1 | |||||||||
| 1 | 1 | |||||||||
| 0 | 0 | |||||||||
| 0 | 0 | |||||||||
| 1 | 1 | |||||||||
| 1 | 1 | |||||||||
| 0 | 0 | |||||||||
| 1 | 1 |
Therefore: xz + x’y’ + y’z’ = xz + y’ is True since both columns have the same values
Answer Ex 23 on page 191
The truth table for a Boolean expression is shown below. Write the Boolean expression in sum of products form. (table is depicted below)
SOLUTION
| X’ | Y’ | Z’ | F | Products | |||
| 1 | (X’y’z’) | ||||||
| 1 | (X’y’z) | ||||||
| 1 | (x’yz’) | ||||||
| 0 | |||||||
| 1 | (xy’z’) | ||||||
| 1 | (xy’z) | ||||||
| 0 | |||||||
| 0 |
F = (X’y’z’) + (X’y’z) + (x’yz’) + (xy’z’) + (xy’z)
Look at Exercise 24 on page 191.
Answer it and show the Truth Table for the one you selected.
Which of the fallowing Boolean expressions is not logically equivalent to all the rest?
a) wx’ + xy’ + xz
b) w + x’ + y’ + z
c) w(x’ + y’ + z)
d) wx’yz’ + wx’y’ + xy’y’ + wz
Given the Truth Table for (xz) + y' [from Ex 13 page 190],
state its Sum of Products expression
then draw the Logic Circuit for that Sum of Products.
xz + x’y’ + y’z’ = xz + y’
Answer Exercise 38 on page 193
SHOW YOUR INTERMEDIATE COLUMNS that lead you to the final column solution.
You should have a column for the output of each Logic Gate.
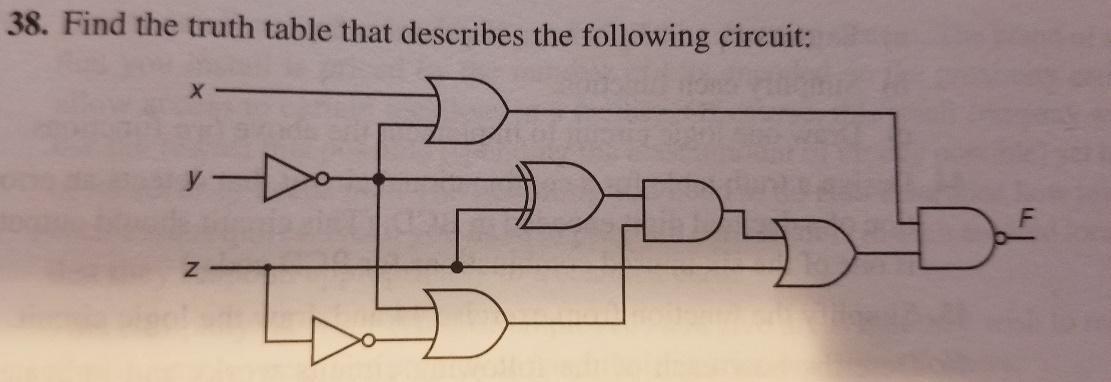
Solution
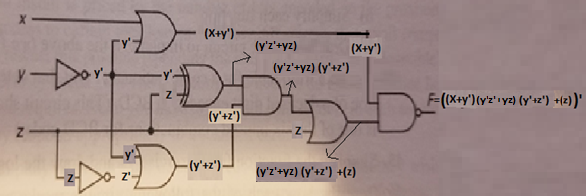
F= ((x+y’)(y’z’+yz)(y’+z’)+(z))’
Answer Exercise 37 on page 192
For guidance, look at Exercise 36 and its solution on page 837.
SHOW YOUR INTERMEDIATE COLUMNS that lead you to the final column solution.
You should have a column for the output of each Logic Gate.
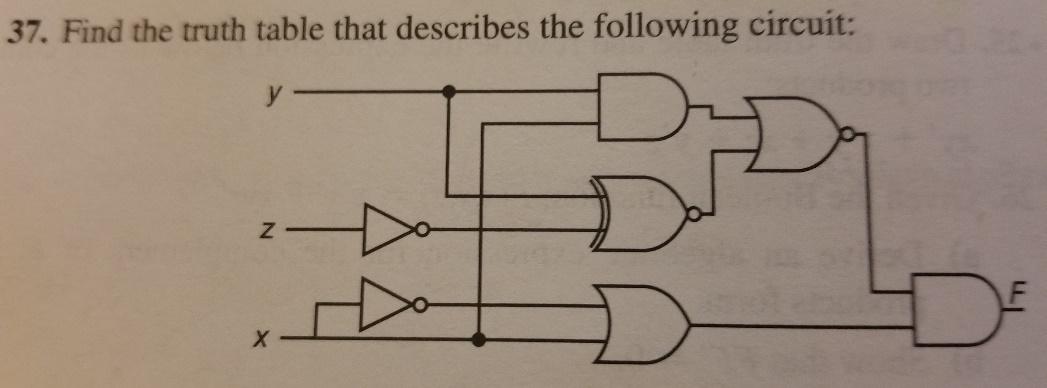
Solution
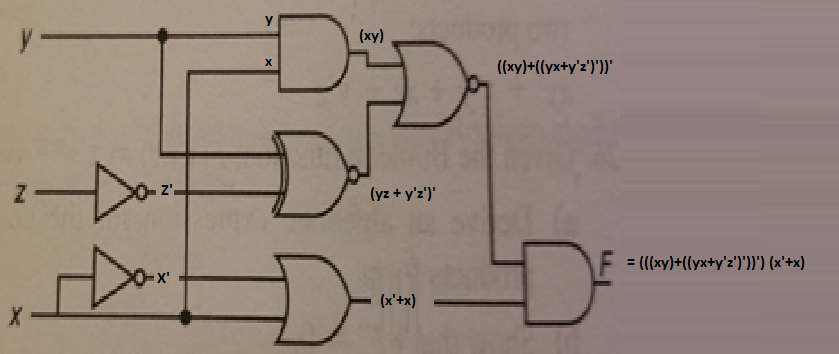
F= (((xy)+((xy+y’z’)’))’(x’+x)



