Need help 2 assignments ten questions each

Chapter 31 Questions to be graded

1. Do the example data meet the assumptions for the independent samples t -test? Provide a rationale

for your answer.

2. If calculating by hand, draw the frequency distributions of the dependent variable, wages earned.

What is the shape of the distribution? If using SPSS, what is the result of the Shapiro-Wilk test

of normality for the dependent variable?

3. What are the means for two group ’ s wages earned?

4. What is the independent samples t -test value?

5. Is the t -test signifi cant at a = 0.05? Specify how you arrived at your answer.

6. If using SPSS, what is the exact likelihood of obtaining a t -test value at least as extreme or as

close to the one that was actually observed, assuming that the null hypothesis is true?

7. Which group earned the most money post-treatment?

8. Write your interpretation of the results as you would in an APA-formatted journal.

9. What do the results indicate regarding the impact of the supported employment vocational

rehabilitation on wages earned?

10. Was the sample size adequate to detect signifi cant differences between the two groups in this

example? Provide a rationale for your answer.

Data set for chapter 31

Need help 2 assignments ten questions each 1

One of the most common statistical tests chosen to investigate signifi cant differences

between two independent samples is the independent samples t -test. The samples are

independent if the study participants in one group are unrelated or different participants

than those in the second group. The dependent variable in an independent samples t -test

must be scaled as interval or ratio. If the dependent variable is measured with a Likert

scale, and the frequency distribution is approximately normally distributed, these data

are usually considered interval level measurement and are appropriate for an independent

samples t -test ( de Winter & Dodou, 2010 ; Rasmussen, 1989 ).

RESEARCH DESIGNS APPROPRIATE FOR THE INDEPENDENT

SAMPLES t- TEST

Research designs that may utilize the independent samples t -test include the randomized

experimental, quasi-experimental, and comparative designs ( Gliner, Morgan, & Leech,

2009 ). The independent variable (the “grouping” variable for the t- test) may be active or

attributional. An active independent variable refers to an intervention, treatment, or

program. An attributional independent variable refers to a characteristic of the participant,

such as gender, diagnosis, or ethnicity. Regardless of the nature of the independent

variable, the independent samples t -test only compares two groups at a time.

Example 1: Researchers conduct a randomized experimental study where the participants

are randomized to either a novel weight loss intervention or a placebo. The number

of pounds lost from baseline to post-treatment for both groups is measured. The research

question is: “Is there a difference between the two groups in weight lost?” The active

independent variable is the weight loss intervention, and the dependent variable is number

of pounds lost over the treatment span.

Null hypothesis: There is no difference between the intervention and the control groups

in weight lost.

Example 2: Researchers conduct a retrospective comparative descriptive study where a

chart review of patients is done to identify patients who recently underwent a colonoscopy.

The patients were divided into two groups: those who used statins continuously in

the past year, and those who did not. The dependent variable is the number of polyps

found during the colonoscopy, and the independent variable is statin use . Her research

question is: “Is there a signifi cant difference between the statin users and nonusers in

number of colon polyps found?”

Null hypothesis: There is no difference between the two groups in number of colon polyps

found.

EXERCISE

350 EXERCISE 31 • Calculating t-tests for Independent Samples

STATISTICAL FORMULA AND ASSUMPTIONS

Use of the independent samples t -test involves the following assumptions ( Zar, 2010 ):

1. Sample means from the population are normally distributed.

2. The dependent variable is measured at the interval/ratio level.

3. The two samples have equal variance.

4. All observations within each sample are independent.

The formula and calculation of the independent samples t -test are presented in this

exercise.

The formula for the independent samples t -test is:

X X

−

−

1 2

s 1 2

where

X1 mean of group1

X2 mean of group 2

“sX1−X 2 ” to the standard error of the difference between the two groups

To compute the t -test, one must compute the denominator in the formula, which is

the standard error of the difference between the means. If the two groups have different

sample sizes, then one must use this formula:

n s n s

n n n n X1 X2

1 1

2 2

1 2 1 2

1 1

−

−−

−

⎛

⎝⎜⎞

⎠⎟

where

n 1 = group 1 sample size

n 2 = group 2 sample size

s 1 = group 1 variance

s 2 = group 2 variance

If the two groups have the same number of subjects in each group, then one can use

this simplifi ed formula:

s s

n X1 X2

−

where

n the sample size in each group and not the total sample of both groups

HAND CALCULATIONS

A randomized experimental study examined the impact of a special type of vocational

rehabilitation on employment variables among spinal cord injured veterans, in which

Calculating t-tests for Independent Samples • EXERCISE 31 351

post-treatment wages and hours worked were examined ( Ottomanelli et al., 2012 ). Participants

were randomized to receive supported employment or treatment as usual (subsequently

referred to as “Control”). Supported employment refers to a type of specialized

interdisciplinary vocational rehabilitation designed to help people with disabilities obtain

and maintain community-based competitive employment in their chosen occupation

( Bond, 2004 ).

The data from this study are presented in Table 31-1 . A simulated subset was selected

for this example so that the computations would be small and manageable. In actuality,

studies involving independent samples t- tests need to be adequately powered ( Aberson,

2010 ; Cohen, 1988 ). See Exercises 24 and 25 for more information regarding statistical

power.

TABLE 31-1 POST-TREATMENT WEEKLY HOURS WORKED BY TREATMENT AND

CONTROL GROUPS

Participant # Weekly Hours Worked Participant # Weekly Hours Worked

Treatment Group Treatment Group Control Group Control Group

1 25 11 8

2 27 12 9

3 19 13 15

4 20 14 17

5 40 15 24

6 25 16 15

7 40 17 18

8 35 18 9

9 30 19 18

10 15 20 16

The independent variable in this example is the treatment (or intervention) Supported

Employment Vocational Rehabilitation, and the treatment group is compared with the

control group that received usual or standard care. The dependent variable was number

of weekly hours worked post-treatment. The null hypothesis is: “There is no difference

between the treatment and control groups in post-treatment weekly hours worked among

veterans with spinal cord injuries.”

The computations for the independent samples t- test are as follows:

Step 1: Compute means for both groups, which involves the sum of scores for each group

divided by the number in the group.

The mean for Group 1, Treatment Group: X1 27.6

The mean for Group 2, Control Group: X2 14.9

Step 2: Compute the numerator of the t -test:

27.6 −14.9 12.7

It does not matter which group is designated as “Group 1” or “Group 2.”

Another possible correct method for Step 2 is to subtract Group 1 ’ s mean from Group

2 ’ s mean, such as: X2 −X1: 14.9 − 27.6 = −1 2.7

This will result in the exact same t -test results and interpretation, only the t -test value

will be negative instead of positive. The sign of the t -test does not matter in the

interpretation of the results—only the magnitude of the t -test.

352 EXERCISE 31 • Calculating t-tests for Independent Samples

Step 3: Compute the standard error of the difference.

a. Compute the variances for each group:

s² for Group174.71

s² for Group 2 24.99

b. Plug into the standard error of the difference formula:

s s

X X

1 2

74 71 24 99

−





. .

3.16

Step 4: Compute t value:

X X

−



−

1 2

12 7

3 16

t 4.02

Step 5: Compute the degrees of freedom:

df n n

−



1 2 2

10 10 2

Step 6: Locate the critical t value in the t distribution table ( Appendix A ) and compare it

to the obtained t value.

The critical t value for a two-tailed test with 18 degrees of freedom at alpha ( α ) = 0.05

is 2.101. This means that if we viewed the t distribution for df = 18, the middle 95% of the

distribution would be marked by − 2.10 and 2.10. The obtained t is 4.02, exceeding the

critical value, which means our t -test is statistically signifi cant and represents a real difference

between the two groups. Therefore, we can reject our null hypothesis. It should

be noted that if the obtained t was − 4.02, it would also be considered statistically signifi -

cant, because the absolute value of the obtained t is compared to the critical t tabled value.

Hours Worked Per Week Control 10 27.60 8.644 2.733

Supported Employment 10 14.90 4.999 1.581

Observe the means for the two groups

Independent Samples Test

Levene's Test for Equality of

Variances t-test for Equality of Means

F Sig. t df Sig. (2-tailed)

Mean

Difference

Std. Error

Difference

95% Confidence Interval of the

Difference

Lower Upper

Hours Worked Per Week Equal variances assumed 3.267 .087 4.022 18 .001 12.700 3.158 6.066 19.334

Equal variances not

assumed

4.022 14.415

.001

12.700 3.158 5.946 19.454

Observe that the t value is 4.022 The exact p value is .001

Step 2: Move the independent variable, Group, into the space titled “Grouping Variable.”

Click “Defi ne Groups” and enter 1 and 0 to represent the coding chosen to differentiate

between the two groups. Click Continue and OK.

INTERPRETATION OF SPSS OUTPUT

The following tables are generated from SPSS. The fi rst table contains descriptive statistics

for hours worked, separated by the two groups. The second table contains the t- test

results.

T-Test

The fi rst table displays descriptive statistics that allow us to observe the means for both

groups. This table is important because it indicates that the participants in the treatment

group (Supported Employment) worked 27.60 weekly hours on average, and the participants

in the Control group worked 14.90 weekly hours on average.

Calculating t-tests for Independent Samples • EXERCISE 31 355

The last table contains the actual t -test value, the p value, along with the values that

compose the t -test formula. The fi rst value in the table is the Levene ’ s test for equality of

variances. The Levene ’ s test is a statistical test of the equal variances assumption. The

p value is 0.087, indicating the there was no signifi cant difference between the two groups ’

variances. If there had been a signifi cant difference, the second row of the table, titled

“Equal variances not assumed,” would be reported in the results.

Following the Levene ’ s test results are the t -test value of 4.022 and the p value of .001,

otherwise known as the probability of obtaining a statistical value at least as extreme or

as close to the one that was actually observed, assuming that the null hypothesis is true.

Following the t -test value, the next value in the table is 12.70, which is the mean difference

that we computed in Step 2 of our hand calculations. The next value in the table is 3.16,

the value we computed in Steps 3a and 3b of our hand calculations.

FINAL INTERPRETATION IN AMERICAN PSYCHOLOGICAL

ASSOCIATION (APA) FORMAT

The following interpretation is written as it might appear in a research article, formatted

according to APA guidelines (APA, 2010). An independent samples t -test computed on

hours worked revealed that veterans who received supported employment worked signifi -

cantly more hours post-treatment than veterans in the control group, t (18) = 4.02, p =

0.001; X = 27.6 versus 14.9, respectively. Thus, the particular type of vocational rehabilitation

approach implemented to increase the work activity of spinal cord injured veterans

appeared to have been more effective than standard practice.

DATA FOR ADDITIONAL COMPUTATIONAL PRACTICE FOR

QUESTIONS TO BE GRADED

Using the same example from Ottomanelli and colleagues (2012) , participants were randomized to

receive the Supported Employment treatment or usual care (“Control”). A simulated subset was

selected for this example so that the computations would be small and manageable. The independent

variable in this example is the type of treatment received (Supported Employment) or the

Control group and the dependent variable was the amount of weekly wages earned post-treatment.

The null hypothesis is: “There is no difference between the treatment and control groups in posttreatment

weekly wages earned among veterans with spinal cord injuries.”

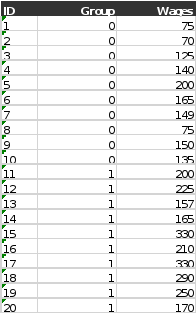
Compute the independent samples t- test on the data in Table 31-2 below.

Weekly Wages Earned

Treatment Group Treatment Group Control Group Control Group

1 $200 11 $75

2 $225 12 $70

3 $157 13 $125

4 $165 14 $140

5 $330 15 $200

6 $210 16 $165

7 $330 17 $149

8 $290 18 $75

9 $250 19 $150

10 $170 20 $135

Chapter 32 Questions to be graded:

1. Do the example data meet the assumptions for the paired samples t -test? Provide a rationale for

your answer.

2. If calculating by hand, draw the frequency distributions of the two variables. What are the shapes

of the distributions? If using SPSS, what are the results of the Shapiro-Wilk tests of normality

for the two variables?

3. What are the means for the baseline and posttreatment affective distress scores, respectively?

4. What is the paired samples t -test value

5. Is the t -test signifi cant at α = 0.05? Specify how you arrived at your answer.

6. If using SPSS, what is the exact likelihood of obtaining a t- test value at least as extreme as or as

close to the one that was actually observed, assuming that the null hypothesis is true?

7. On average, did the affective distress scores improve or deteriorate over time? Provide a rationale

for your answer.

8. Write your interpretation of the results as you would in an APA-formatted journal.

9. What do the results indicate regarding the impact of the rehabilitation on emotional distress

levels?

10. What are the weaknesses of the design in this example?

Chapter 32 Data set:

id	DistressBaseline	DistressPost
001	0.80	0.70
002	3.60	1.70
003	0.30	1.30
004	4.30	3.00
005	2.00	1.30
006	2.30	2.70
007	3.00	1.30
008	3.90	1.70
009	4.90	3.00
010	5.20	3.70

TABLE 2 AFFECTIVE (EMOTIONAL) DISTRESS LEVELS AT BASELINE AND

POST-TREATMENT

DATA FOR ADDITIONAL COMPUTATIONAL PRACTICE FOR

QUESTIONS TO BE GRADED

Using an example from a study examining the level of functional impairment among 10 adults

receiving rehabilitation for a painful injury, changes over time were investigated ( Cipher, Kurian,

Fulda, Snider, & Van Beest, 2007 ). The dependent variable is emotional distress, which was represented

by patients ’ scores on the Affective Distress subscale of the Multidimensional Pain Inventory

(MPI; Kerns, Turk, & Rudy, 1985), with higher scores representing more emotional distress due to

pain. The null hypothesis is: “There is no signifi cant reduction in emotional distress from baseline

to post-treatment for patients in a rehabilitation program.”

Compute the paired samples t- test on the data in Table 2 below.

-Participant #

-Baseline Affective

Distress Scores

-Post-treatment Affective

Distress

-Difference

Scores

1/ .8/ .7/ .1

2 /3.6 /1.7/ 1.9

3/ .3 / 1.3 /-1.0

4 /4.3/ 3.0 /1.3

5/ 2.0/ 1.3 /.7

6 /2.3/ 2.7/- .4

7/ 3.0/ 1.3/ 1.7

8/ 3.9/ 1.7/ 2.2

9/ 4.9/ 3.0/ 1.9

10/ 5.2/ 3.7 /1.5

A paired samples t -test (also referred to as a dependent samples t -test) is a statistical procedure

that compares two sets of data from one group of people. The paired samples t -test

was introduced in Exercise 17 , which is focused on understanding these results in research

reports. This exercise focuses on calculating and interpreting the results from paired

samples t -tests. When samples are related, the formula used to calculate the t statistic is

different from the formula for the independent samples t -test (see Exercise 31 ).

RESEARCH DESIGNS APPROPRIATE FOR THE PAIRED

SAMPLES t -TEST

The term paired samples refers to a research design that repeatedly assesses the same group

of people, an approach commonly referred to as repeated measures . Paired samples can

also refer to naturally occurring pairs, such as siblings or spouses. The most common

research design that may utilize a paired samples t -test is the one-group pretest-posttest

design, wherein a single group of subjects is assessed at baseline and once again after

receiving an intervention ( Gliner, Morgan, & Leech, 2009 ). Another design that may

utilize a paired samples t -test is where one group of participants is exposed to one level

of an intervention and then those scores are compared with the same participants ’

responses to another level of the intervention, resulting in paired scores. This is called a

one-sample crossover design ( Gliner et al., 2009 ).

Example 1: A researcher conducts a one-sample pretest-posttest study wherein she

assesses her sample for health status at baseline, and again post-treatment. Her research

question is: “Is there a difference in health status from baseline to post-treatment?” The

dependent variable is health status.

Null hypothesis: There is no difference between the baseline and post-treatment health

status scores.

Example 2: A researcher conducts a crossover study wherein subjects receive a randomly

generated order of two medications. One is a standard FDA-approved medication to

reduce blood pressure, and the other is an experimental medication. The dependent variable

is reduction in blood pressure (systolic and diastolic), and the independent variable

is medication type. Her research question is: “Is there a difference between the experimental

medication and the control medication in blood pressure reduction?”

Null hypothesis: There is no difference between the two medication trials in blood pressure

reduction.

EXERCISE

364 EXERCISE 32 • Calculating t-tests for Paired (Dependent) Samples

STATISTICAL FORMULA AND ASSUMPTIONS

Like the independent samples t- test, this t -test requires that differences between the

paired scores be independent and normally or approximately normally distributed (see

Exercise 17 ).

The formula for the paired samples t -test is:

t D

where:

D the mean difference of the paired data

sD the standard error of the difference 

To compute the t -test, one must compute the denominator in the formula: the standard

error of the difference:

n D

D

where:

sD the standard deviation of the differences between the paired data

n the number of subjects in the sample or number of paired scores in the case of sibling or

spousal data





HAND CALCULATIONS

Using an example from a study examining the dental pocket depths among 10 adults

receiving treatment for periodontitis, changes over time were investigated ( Pope,

Rossmann, Kerns, Beach, & Cipher, 2014 ). These data are presented in Table 32-1 . A simulated

subset was selected for this example so that the computations would be small and

manageable. In actuality, studies involving paired samples t- tests need to be adequately

powered ( Aberson, 2010 ; Cohen, 1988 ). See Exercises 24 and 25 for more information

regarding statistical power.

AT BASELINE AND POST-TREATMENT

Participant #

Baseline Probing

Depths (mm)

Post-treatment Probing

Depths (mm)

Difference

Scores

1/ 5/4 /1

2/ 4/ 2/ 2

3 /5/ 3 /2

4 /6 /3 3

5/ 5/ 3/ 2

6 /4/ 2/ 2

7/ 5/ 4/ 1

8/ 6/ 4/ 2

9 /7/ 5/ 2

10/ 5/ 3/ 2