Will need to be completed on separate paper.
Name: Period:
Unit 6: Exploration of Polygon & Quadrilateral Properties
| Date | Topic | Assignment |
| Tues. Jan 7 | REVIEW: Perimeter & Area | p. 2 & 3 |
| Wed. Jan. 8 | Day 1: Polygon & Quadrilateral Properties Notes | Page 4 |
| Thurs. Jan. 9 | Day 2: Sum of Interior & Exterior Angles Practice | Page 6 |
| Fri. Jan. 10 | Day 3: Sum of Interior & Exterior Angles Practice | Page 7 |
| Mon. Jan. 13 | Day 4: Quadrilateral Property Notecard | Page 8 |
| Wed. Jan. 14 | Day 5: Parallelograms | Page 10 |
| Thurs. Jan. 15 | Day 6: Rectangles /Squares | Page 13 |
| Fri. Jan. 16 | Day 7: Rhombus/Kite | Page 15 |
| Mon. Jan. 20 | NO SCHOOL: MLK Holiday | |
| Tues. Jan 21 | Day 8: Trapezoids | Page 17 |
| Wed. Jan. 22 | Day 9: Proofs | Page 21 |
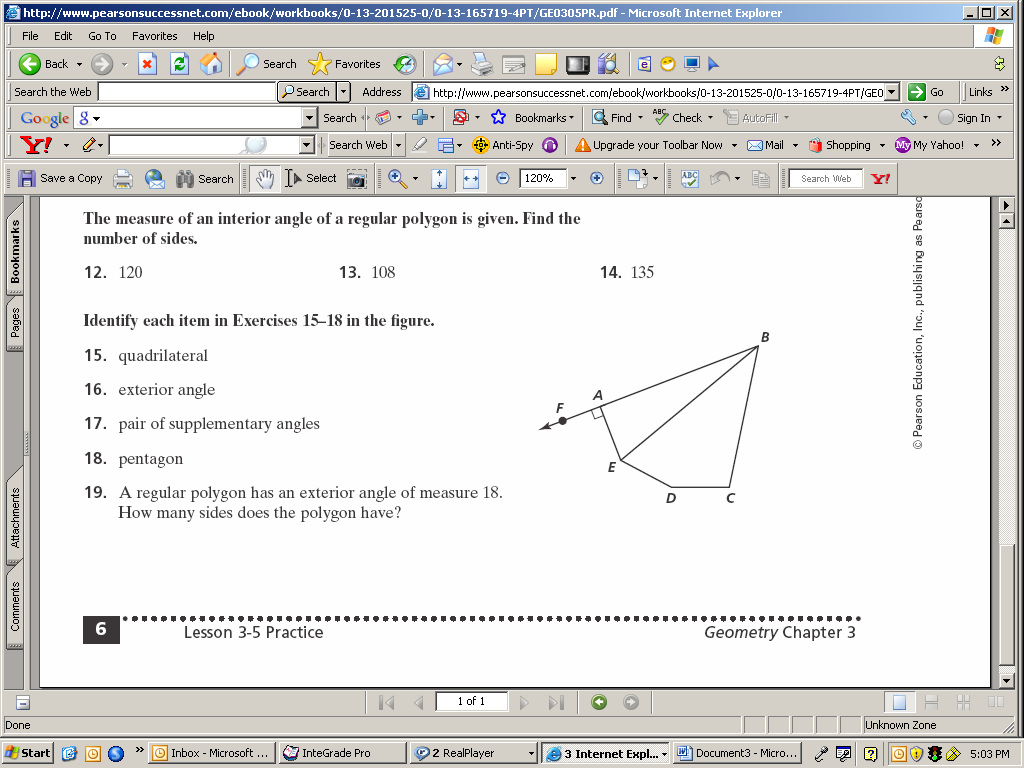
| Thurs. Jan. 23 | Day 10: UNIT 6 REVIEW | Distributed Separately |
| Fri. Jan. 24 | UNIT 6 EXAM | Distributed Separately |

REVIEW: Perimeter/Area
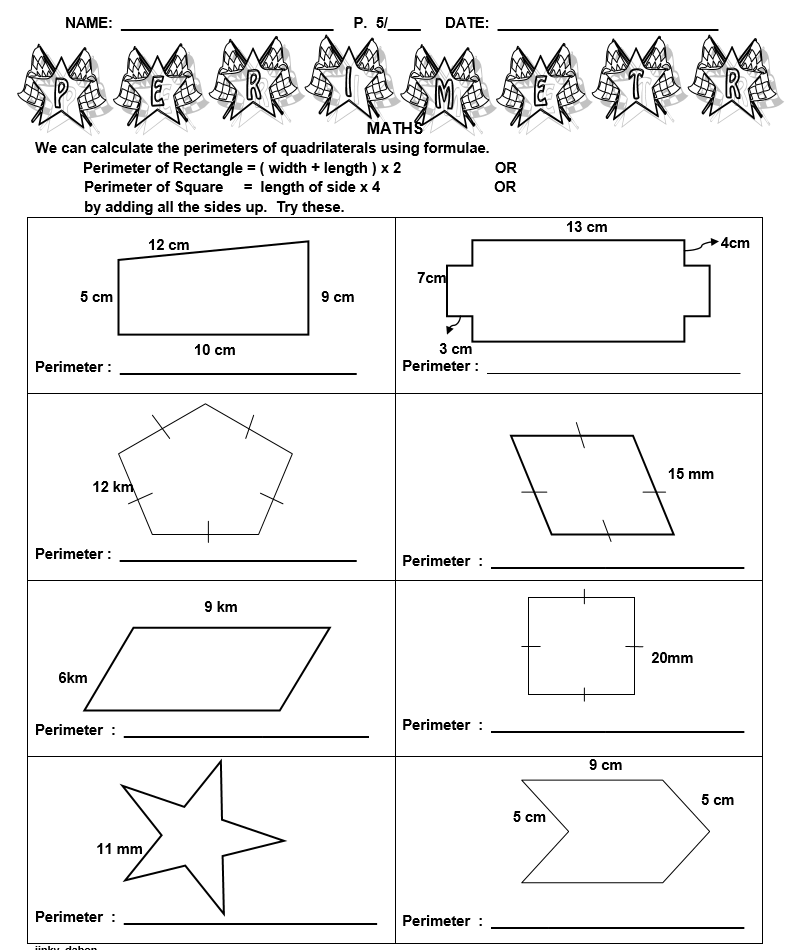
REVIEW: Perimeter/Area
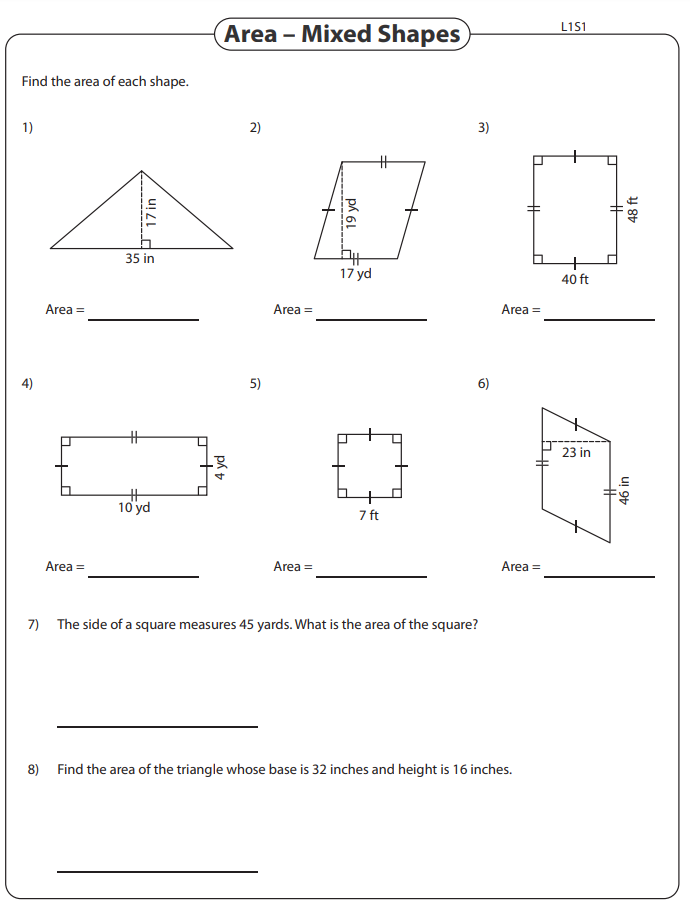
Day 1: Polygon & Quadrilateral Properties Notes
Notes on Polygons:
*A polygon is a figure made up of straight lines that do not intersect.
Tell whether each figure below is a polygon or not. Write “yes” or “no” beneath each figure.
There are two types of polygons: Concave & Convex
Concave polygons look like they are “caving in”. Convex polygons look like the “normal” polygons you are used to seeing. Write “concave” or “convex” beneath each polygon below.
Polygons are named according to their number of sides. See how many you can name.
3 – 8 –
4 – 9 –
5 – 10 –
6 – 11 –
7 – 12 -
*When there are 13 + sides we call this an “n – gon” where “n” is the number of sides.
i.e. 26 sided polygon is called a __________________.
*Regular Polygon – a convex polygon that has equal _________ & equal s.
Ex: Regular triangle is called an _______________________
Ex: Regular quadrilateral is called a ___________________
Interior & Exterior Angles
Each arrow is pointing to an angle. Label the angle each arrow is pointing to as
“interior” or “exterior”.
What is the relationship between an interior and exterior angle of
a polygon? ____________________________________
I + E = ________
Sum of Interior Angles:
The sum of the interior angles for a polygon changes depending on how many sides the polygon has.
*Create as many triangles as possible without overlapping in each polygon.
4 sides = ___ triangles
____ fewer triangles than the # of sides
5 sides = ___ triangles
7 sides = ___ triangles
If n represents the number of sides of a polygon, write a formula for how to find the sum of the interior angles for a polygon with n sides. (Hint: the sum of the interior angles for a triangle is ___________)
Formula for SOI (sum of interior s):
SOI =
Ex: Find the sum of the interior angles for a 26-gon.
What would be the measure of ONE interior angle for a 26-gon?
Sum of Exterior Angles of a Polygon (SOE):
Day 2: Sum of Interior & Exterior Angles
*Remember that a regular polygon means all sides and all angles are equal…
Formulas:
1) SOI = (n – 2)180 2) I + E = 180 3) SOE = 360°
4) I = 5) E =
6) n =
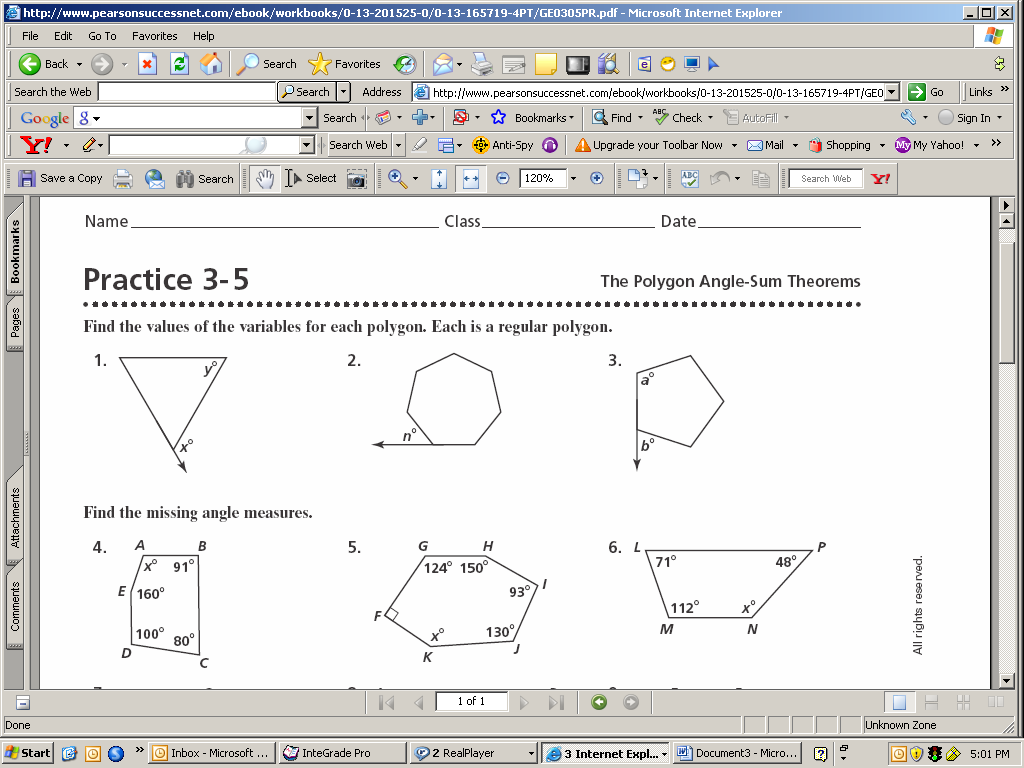
Find the sum of the interior angles for each polygon.
1. 2. Dodecagon 3. Decagon 4. 20-gon
Find the missing angle measures.
5. 6. 7.
8. 9. 10.
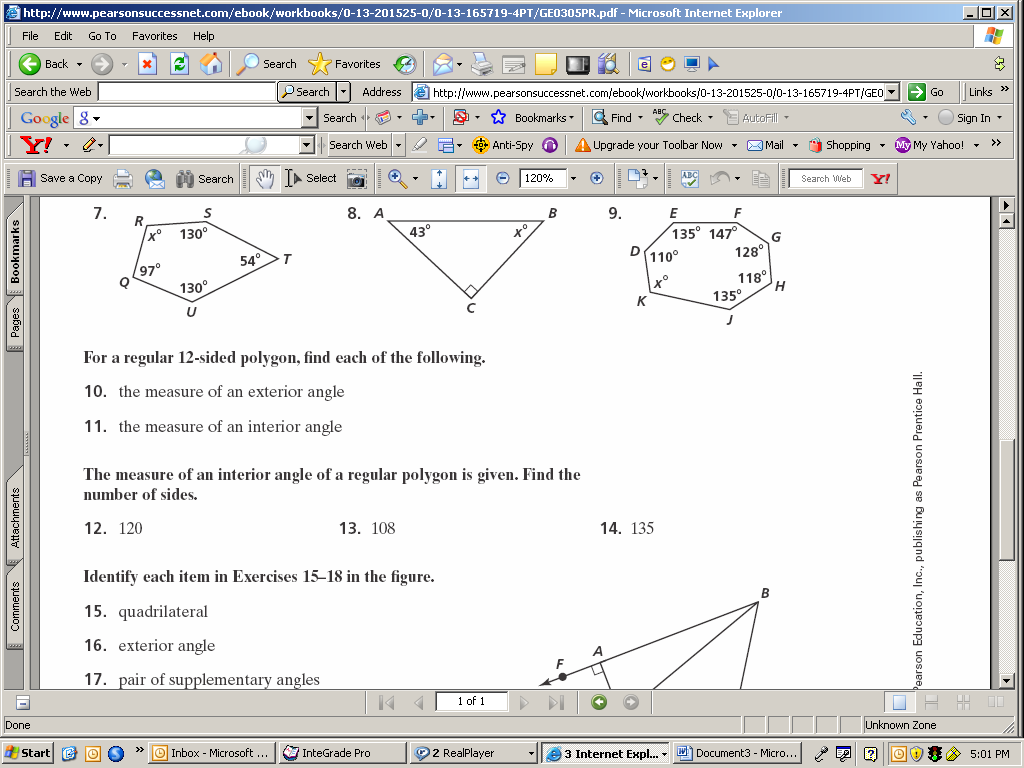
Find the measure of an interior angle and an exterior angle of each regular polygon.
11. Pentagon 12. Dodecagon 13. 18-gon 14. 100-gon
The sum of the measures of the angles of a polygon with n sides is given. Find n.
15. 1080 16. 1980
The measure of an exterior angle of a regular polygon is given. Find the measure of an interior angle, and find the number of sides.
17. 72 18. 18
Day 3: Sum of Interior & Exterior Angles Practice Continued

Day 4 Quadrilateral Properties (Notecard)
1. Parallelogram:
-diagonals: long intersects short at midpoints (not at 90°)
2. Rectangle:
-diagonals: long intersects long at midpoints (not at 90°)
3. Rhombus:
-diagonals: long intersects short at midpoints at 90°
4. Square:
-diagonals: short intersects short at midpoints at 90°
5. Isosceles Trapezoid:
-diagonals: long intersects long (not at midpoint)
6. Kite:
-diagonals: long intersects short at 90° (at midpoint of short, but not midpoint of long)
Quadrilateral
Day 5: Parallelograms
| Properties of a parallelogram: |
|
|
|
|
|
Classify each statement as true or false.
1. Every quadrilateral is a parallelogram.
2. Every parallelogram is a quadrilateral.
3. If quadrilateral RSTW is a parallelogram, then .
4. If quadrilateral DEFG is a parallelogram, then //
.
5. There exists a parallelogram with all sides congruent.
6. There exists a parallelogram ABCD such that m∠A = 70 and m∠C = 80.
7. is a diagonal of parallelogram WXYZ.
Exercises #10-15 refer to parallelogram RSTW. Complete each statement.
8. //_____ 12. ∆RST≅______
9. ≅_____ 13.
_____
10. ≅_____
11. ∠WRS≅_____
Exercises #16-21 refer to parallelogram CDEF.
14. CE = 12, CX = _____
15. FX = 8, FD = _____
16. m∠CDE = 72, m∠EFC = _____
17. m∠1 + m∠2 = 106, m∠FCD = _____
18. m∠3 = 88, m∠2 = _____
19. m∠4 = 41, m∠1 = _____
In each parallelogram, find the indicated measure.
20. Find AD. 21. Find HI.
5x + 4
22. Find m∠R.
Use parallelogram ABCD to answer the following questions.
23. If AB = 12, what other side has a length of 12?
27. If m∠ADC = 29, what is m∠CBA?
28. Does AB + BC = AD + DC?
29. Are ∠DCB and ∠ABC supplementary?
30. If BD = 2x + 8, then XD = _______.
31. If the perimeter of parallelogram ABCD is 72 and BC = 6.5, then AB = _______.
32. Is point X the midpoint of both and
?
Proving Quads are Parallelograms
State whether the information given about quadrilateral SMTP is sufficient to prove that it is a parallelogram.
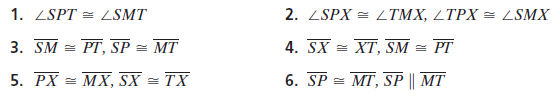
Find the value of x. Then tell whether the figure must be a parallelogram. Explain your answer in a complete sentence.

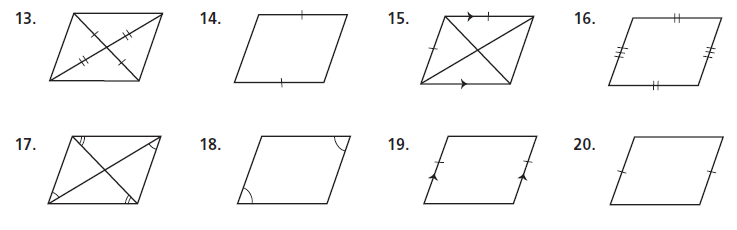
Decide whether the quadrilateral is a parallelogram. Explain your answer in a complete sentence.
Day 6:Rectangles & Squares
| Properties of a rectangle: | Properties of a Square: |
|
|
|
|
|
|
|
|
|
|
| AND | AND |
|
|
|
|
|
Given: ABCD is a rectangle. Name all the parts that make true statements.
1. ≅
Problems #1-12
2. AD =
3. m∠BEC =
4. ≅
5. ⊥
6. ∆ABD≅
7. ∆BEC≅
Answer True or False.
8.
9. bisects
10. bisects ∠BAD
11.
12.
13. WXYZ is a rectangle.
The perimeter of ∆XYZ = 24.
XY + YZ = 5x – 1
XZ = 13 – x
Find WY.
Given: ABCD is a square. Answer True or False.
15.
16. bisects
17. bisects ∠BAD
18.
19.
20. SQRE is a square. The diagonals of SQRE intersect at A. Find:
a) m∠RSQ
b) m∠EAR
c) EA = 5x – 3, RA = 4x + 6. Find EQ
21. WXYZ is a square.
WX = 1 – 10x
YZ = 14 + 3x
Find YW.
22. ABCD is a rectangle. F lies on . E lies on
. mBAF = 29 and mDAE = 39. Find mFAE.
23. In rectangle ABCD, AB = 15 and BC = 6. Find the length of the diagonal.
24. In rectangle ABCD, diagonals and
intersect at E. If AE = 2x – 6y, EC = 2x + 6, and BD = 16, find x & y.
25. In rectangle ABCD, mBAD = 2(mDAC) + 38˚. Find mBAC.
Day 7: Rhombus & Kite
| Properties of a Rhombus: | Properties of a kite: |
|
|
|
|
|
|
| |
| |
| AND | |
| |
| |
1. Given: ABCD is a rhombus.
m∠3 = 56
Find:
m∠1 m∠7
m∠2 m∠8
m∠3 m∠9
m∠4 m∠10
m∠5 m∠11
m∠6 m∠12
2. Given: BDEG is a rectangle. ABCD is a rhombus.
Find:
a) m∠DAB
b) m∠BCG
c) m∠GCF
d) m∠DEG
WXYZ is a rhombus. (#3-4)
3. m∠X = 24(10 – x), m∠Z = 6(x + 15), find m∠Y. 4. WX = 3x + 2, XY = 5x − 10, find YZ.
5. Answer always, sometimes, or never.
a. If a quadrilateral is a rhombus, then it is _______________ a square.
b. If a quadrilateral is a square, then it is ________________ a rectangle.
c. If a rectangle is a rhombus, then it is _________________ a square.
d. If a quadrilateral is a rhombus, then it is __________________ a regular polygon.
6. Answer true or false.
a. Every rectangle is a parallelogram. b. The diagonals of a rhombus are perpendicular.
c. Every rhombus is a regular polygon. d. If a rectangle is equilateral, then it is a square.
7. Find the measure of each numbered angle. 8. Find the perimeter of the kite.
9. The following ordered pairs represent the endpoints of one diagonal of a kite (they are not all from the same kite).
Find the midpoint of the diagonal. Find the length of the diagonal with the given endpoints.
a. (6, 4); (12, 2) b. (4, 5); (3, 2)
Find the slopes of the diagonals with the given endpoints.
c. (1, 2); (1, 1) d. (2, 3); (2, 3)
KITE is a kite. (Probs. #10, 11)
10. If mKIE = 50 and mKEI = x + 5(x − 2), find x.
11. If m11 = 4x and m10 = x + 10, find m8.
12. ABCD is a rhombus with diagonals AC and DB intersecting at R. If mBRC = 2x2 + 40, find x.
13. ABCD is a rhombus with diagonals AC and DB intersecting at R. If mADB = 2x − 1, mARB = 6x, mACB = y, find x and y.
Day 8: Trapezoids
| Properties of a trapezoid: | Properties of Isosceles Trapezoid: |
|
|
| |
|
Find the measures of the other angles.
2. In the isosceles trapezoid, m A = 5k.
Find the measures of the other angles in
terms of k. Problems #1 and 2
3. Find the lengths of the legs of isosceles trapezoid ABCD if A(0, 0) B(5, 0) C(3, 3) and D (2, 3).
4. Given: Isosceles trapezoid ABCD
mBAC = 30, mDBC = 85
Find: m1 m6 mDAB
m2 m7 mCBA
m3 m8
m4 mADC
m5 mBCD
5. Given: Isosceles trapezoid JXVI
mJVI = 42, mIJV = 65
Find: m1 m6 m10
m2 mJIV m11
m3 m7 m12
m4 m8 mIJX
m5 m9
Find the value(s) of the variable(s) in each isosceles trapezoid.
6. 7. 8.
Y°
(6x+20)°
3x − 3
7x
2x+5
(4x)°
x − 1
Each trapezoid is isosceles. Find the measure of each angle.
9. 10.
77°
105°
Find the value of the variable in each isosceles trapezoid.
11. 12. 13.
(3x+15)°
60°
3x°
45°
TV = 2x − 1
US = x + 2
14. Given: Isosceles trapezoid JXVI
mIXV = 83, mVJX = 28
Find: m1 m6 m10
m2 mIVX m11
m3 m7 m12
m4 m8 mVXJ
m5 m9



Day 9: Proofs
1. Given: ABCD is a rectangle
ACBE is a parallelogram
Prove: DB EB
Statements Reasons
1. ABCD is a rectangle 1.
2. DB AC 2.
3. ACBE is a parallelogram 3.
4. AC EB 4.
5. DB EB 5.
2. Given: ABCD is a trapezoid with AB // CD
AP bisects DAB
Prove: APD is isosceles
Statements Reasons
1. ABCD is a trapezoid with AB // CD, 1.
AP bisects DAB
2. DPA PAB 2.
3. DAP PAB 3.
4. DPA DAP 4.
5. AD PD 5.
6. APD is isosceles 6.
3. Given: ABCD , FG bisects DB
Prove: DB bisects FG
Statements Reasons
1. ABCD, FG bisects DB 1.
2. CD // BA 2.
3. CDB ABD, DFE BGE 3.
4. BE DE 4.
5. BEG DEF 5.
6. FE GE 6.
7. DB bisects FG 7.
Prove: ∆COD ∆GAT
Statements Reasons
1. CO DG, AG CT 1.
2. COD and TAG are right angles 2.
3. COD TAG 3.
4. CTGD 4.
5. DC GT 5.
6. D T 6.
7. ∆COD ∆GAT 7.
5. Given: Isosceles Trapezoid RSPT
Prove: ∆TPQ is isosceles
Statements Reasons
1. Isosceles Trapezoid RSPT 1.
2. R S 2.
3. RS // TP 3.
4. R PTQ, S TPQ 4.
5. PTQ TPQ 5.
6. TQ PQ 6.
7. TPQ is isosceles 7.



