Bacchus Work NO ONE ELSE

Read Section 11.4, pages 540  547.

Type in the answers below each question and email the completed document to me, or print out the document and fill it out by hand and email a scan or photo of it to me.

1) Looking at example 11.15, figure 11.47, graphs (b) and (c) are isomorphic, so they are the same graph. What is the difference between graphs (b) and (c)?

2) So K4 is a planar graph. Is K5 a planar graph?

3) For which values of n is Qn a bipartite graph?

4) Is K2,3 a planar graph? What about K3,3 ?

5) The graphs in figure 11.51 are clearly non-isomorphic. What word describes the relationship between the 4 graphs in figure 11.51?

6) In figure 11.52, two graphs are shown. What is the relationship between these two graphs, and what does that relationship prove?

7) Why is it not possible to apply Theorem 11.6 to the graphs K3,3 or K5 ?

8) Can a graph with 100 edges and 30 vertices be planar? Explain using Corollary 11.3.

Discrete Structures

Readings Check, section 11.5

Read Section 11.5, pages 556  561. [You do not need to read the proofs.]

Type in the answers below each question and email the completed document to me, or print out the document and fill it out by hand and email a scan or photo of it to me.

1) How does a Hamilton cycle differ from an Euler circuit?

2) For which values of n does Qn have a Hamilton cycle?

3) Does the following graph have a Hamilton cycle?

4) Does the following graph have a directed Hamilton path? [Hint: does Theorem 11.7 apply?]

5) Find a directed Hamilton cycle in the following graph. List the vertices of the cycle in order:

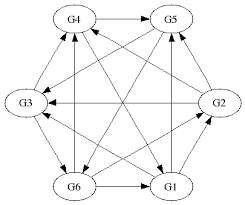
6) Suppose that a loop-free graph G is 10-regular and has 20 vertices. Does G have a Hamilton cycle?

[Hint: use Corollary 11.5.]

Type your answers under the questions given below, or, print out this sheet, use pen or pencil to fill it out, and email a scan or photo of it to the instructor.

1) Suppose that an extensive subway system has 40 stations, and that each station has tracks that directly connect it to 6 other stations. Can this system be built so that no track crosses over any other track? Explain your answer.

2) Is the complete graph K2,100 a planar graph? Justify your answer.

3) What is the minimum number of edges that must be removed from K5 to obtain a planar graph? How about for K6?

4) Is the following a planar graph? [Hint: take one of the triangles outside of the hexagon.]

5) Is the following a planar graph? [Does Kuratowski's theorem apply?]

6) Does the following graph contain a Hamilton cycle that starts at vertex a ? If so, then list the vertices of the cycle in order.

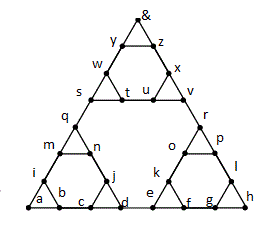
Does it contain a Hamilton cycle that starts at vertex t ? (If yes then no need to list the vertices)

7) If you can find an independent set of vertices I in a graph G in such a way that:

e + 2 | I |  < v

[e = total number of edges in G; v = total number of vertices in G; = sum of degrees of vertices in I.]

Then the graph has no Hamilton cycle.

Find an independent set of vertices I in the following graph that makes the inequality true, thus showing that the graph has no Hamilton cycle. Fill out your answers below.

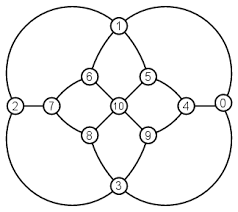
I = e = 2 | I | = = v =

Be sure that your choice of I satisfies e + 2 | I |  < v

Discrete Structures

Readings Check, section 12.1

Read Section 12.1, pages 581  585.

Type in the answers below each question and email the completed document to me, or print out the document and fill it out by hand and email a scan or photo of it to me.

1) Why is G2 in figure 12.1 not a tree? Why is G3 not a tree?

2) If a tree has 1000 vertices, how many edges does it have? [Theorem 12.3]

3) What are pendant vertices? What is the minimum number of pendant vertices that a tree must contain?

4) Examples 12.1 and 12.2 show an interesting application of trees to organic chemistry. If an alkane has 20 carbon atoms, how many hydrogen atoms does it contain?

5) Is it true that every edge in a tree is a bridge? [See also notes for 11.5.]

Discrete Structures

Readings Check, section 12.2

Read Section 12.2, pages 587  603.

Type in the answers below each question and email the completed document to me, or print out the document and fill it out by hand and email a scan or photo of it to me.

1) In a rooted tree, if r is the root, what is id(r)? [Where id(x) is the "in degree" of vertex x, which is the number of vertices pointing toward x and adjacent to x.]

2) In a rooted tree, if v is a vertex other than the root, what is id(v)?

3) In a rooted tree, if v is a vertex with od(v) = 0, what is v called? [Where od(v) is the "out degree" of vertex v, which is the number of vertices that v points to.]

4) In the tree in figure 12.12, what are the children of vertex 3?

5) In the tree in figure 12.12, what is the level of vertex 1.2.3.2?

6) What type of rooted tree has od(v) = 0 or 2 for all vertices?

7) When converting a mathematical expression into Polish (prefix) notation, what symbols are removed from the original expression?

8) In a preorder traversal, what is visited first, the root or the subtrees?

9) In a postorder traversal, what is visited first, the root or the subtrees?

10) In an inorder traversal, three things are visited: root, left subtree, and right subtree. What is the order in which these three are visited?

11) With regard to a graph G = (V, E), what exactly is the purpose of the depth first search?

12) If T is a complete 3-ary tree with 22 vertices, how many internal vertices does T have? [Theorem 12.6]

13) What is the height of the tree in figure 12.24(b)? [definition 12.6]//

14) Using corollary 12.1, what is the height of a balanced complete 4-ary tree with 1025 leaves?

Type your answers under the questions given below, or, print out this sheet, use pen or pencil to fill it out, and email a scan or photo of it to the instructor.

1) How many different (though some may be isomorphic) spanning trees can be found for the graph below?

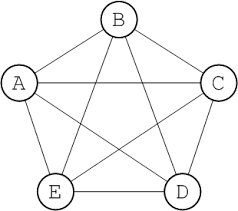
2) Suppose that a tree T has 1000 vertices. How many edges are in the graph ?

3) Evaluate the following expression, which is given in Polish notation:

+  2 ^ + 6 4 3 ^  9 7 + 1  8 5

4) Suppose that a balanced complete ternary (3ary) tree with height 10 has 21683 leaves. How many internal vertices does it have at level 9? [Hint: use the result of 12.2, #20.]

5) The following is called an adjacency matrix for a graph G. The vertices of the graph are 0, 1, 2, … , 9. They are listed on the left side of the rows and at the top of the columns. If two vertices x and y are adjacent, then a 1 will appear where column x meets row y. So for example, vertex 6 is adjacent to vertices 0, 1, and 2. Vertex 8 is adjacent to vertices 0, 3, and 7. Answer the questions below.

a) Does this graph contain any loops?

b) What is the significance of adding the sum of the numbers in a particular column (or row)?

c) How many edges are in the graph?

d) Is the graph G a connected graph? [Hint: you might use the method of example 12.12.]

bonus: For a full binary tree (page 611) of height h, what is the total number of paths that exist going from the root to any other vertex in the tree? For example, if the height is h = 1, there are 2 paths. If h = 2, there are 6 paths, and so on.